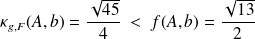Partial LLSP
Motivation
Consider the linear least-squares problem
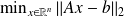
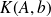measures the sensitivity of the computed solution
to perturbations of the data
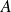and
.
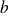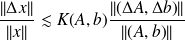
We have from [Gratton 96]
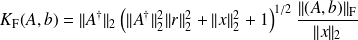
Motivation
Consider the example
parameter estimation
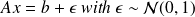
Are some
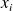more sensitive than others to perturbations of the data ?
More generally if
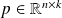
What is the sensitivity of
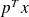to perturbations of
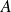and/or
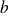
Example : Exemple 1
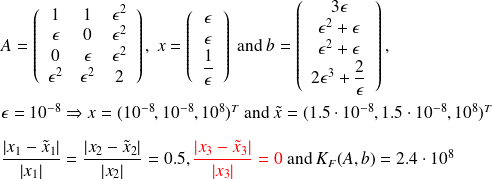
If
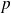is a projection onto
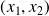or
,
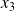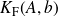does not provide reliable information about the sensitivity of
.
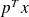Example :
Consider
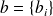depend. on
Approximate with a 3 deg. polynomial such that
Assume perturbations on
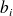of order
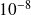. For
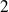computed solutions
and
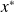, we obtain
whereas
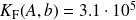
Partial condition number
Definition : Condition number
Let
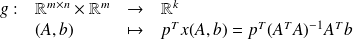
Since
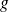is
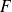-differentiable, we have
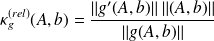
we consider
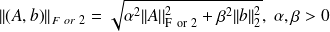
Exact formula in Frobenius norm
Fundamental : Theorem 1
Let
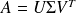the thin singular value decomposition of
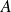with
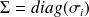and
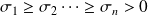. Then
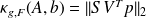where
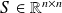is the diagonal matrix with
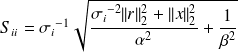
Interpretation
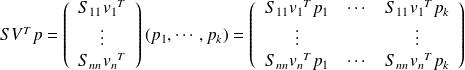
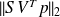is large when there exist large
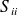and there exist
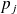such that
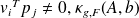
is large when
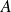has small singular values and
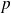has components in the corresponding right singular vectors.
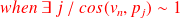
Particular case
If
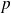is a vector (
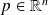), then
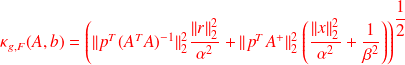
Remark: If we have the
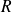factor of the
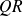decomposition of
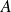then
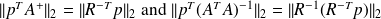
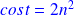
Bounds in spectral and Frobenius norm
Fundamental : Theorem
The absolute condition numbers of
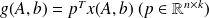in the Frobenius and spectral norms can be respectively bounded as follows
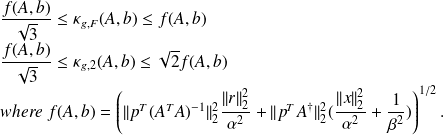
Proof
First note that we have
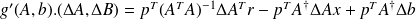
We start by establishing the lower bounds. Let
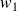and
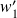(resp.
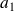and
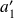$) be right (resp. the left) singular vectors corresponding to the largest singular values of respectively
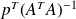and
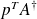. We use a particular perturbation
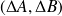expressed as
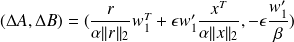, where
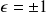
By replacing this value of
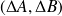in
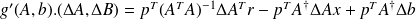we get
.
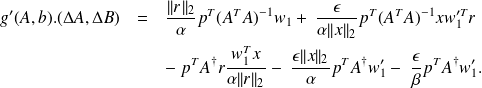Since
we have
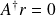. Moreover we have
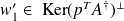and thus
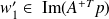and can be written
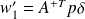for some
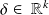. Then
.
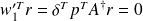It follows that
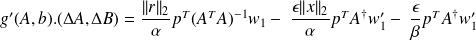
From
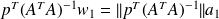and
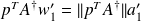, we obtain
.
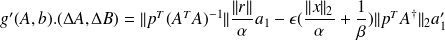Since
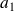and
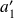are unit vectors,
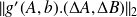can be be developed as
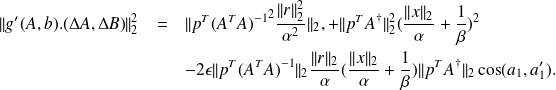
By choosing
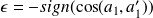the third term of the above expression becomes positive. Furthermore we have
.
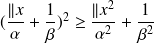Then we obtain
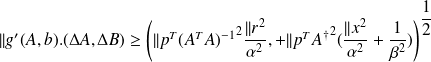i.e
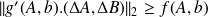.On the other hand, we have
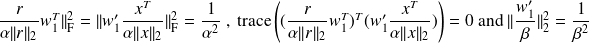
Then
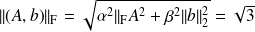and thus
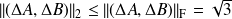
So we have shown that
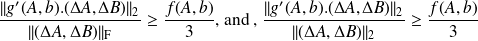for a particular value of
.
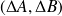This proves that
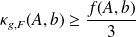and
.
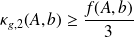Let us now establish the upper bound for
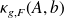. If
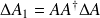and
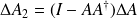, then it comes that
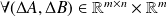
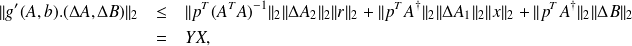
where
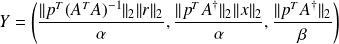
and
.
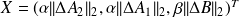Hence
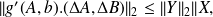
with
.
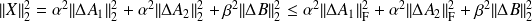Then, since
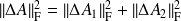, we have
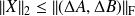and(
) yields
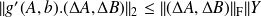which implies that
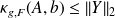or
.
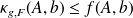An upper bound of
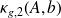can be computed in a similar manner : form the derivative of
,
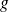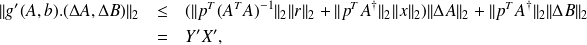
where
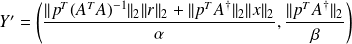and
.
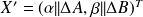Since
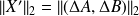we have
.
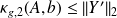Using then the inequality
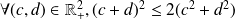we show that
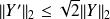and obtain
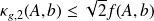which concludes the proof.
Theorem (31)shows that
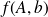can be considered as a very sharp estimate of the partial condition number expressed either in Frobenius or spectral norm. Indeed, it lies within a factor
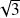of
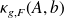or
.
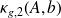Another observation is that we have
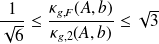. Thus even if the Frobenius and spectral norms of a given matrix can be very different (
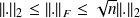), the condition numbers expressed in both norms are of same order.
It results that a good estimate of
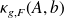is also a good estimate of
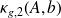. Moreover if the R factor of
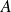is available,
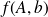can be computed by solving two
by
triangular systems with
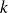right-hand sides and thus the computational cost is
.
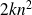Bounds
In the general case where
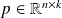, then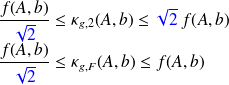
where
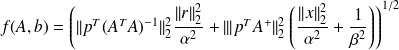
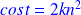
Remark
We show that
.
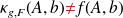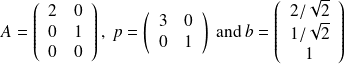
we have
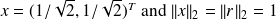
and
