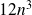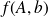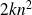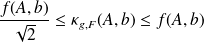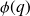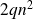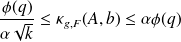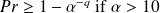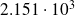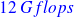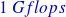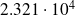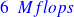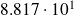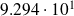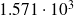Estimates vs exact formula
We assume that the R factor of the QR decomp. of
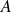is known. Comparison between exact formula and estimates for
| flops | accuracy |
exact formula
|
| exact |
sharp estimate
|
|
|
stat. estimate
|
|
|
Example : Example 1
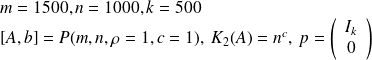
| bound
| stat. estimate
|
|
|
|
Numerical illustration
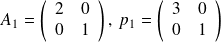
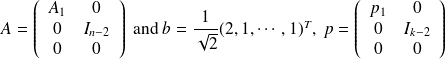
| bound
| stat. estimate
|
|
|
|
Truncated SVD solution
We are interested in the truncated SVD solution
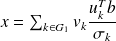.Typically ,
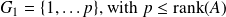
We consider the function
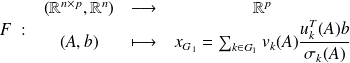
Choice of norms :
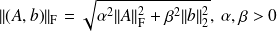and
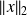
Differentiability of the singular elements of a matrix (I)
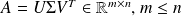
and
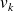are the
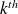singular vectors of
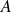
for
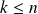, define
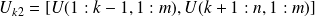, and similarly
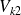
Set also
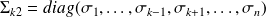and
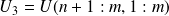
Assume that the singular values
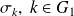are simple and nonzero.
Differentiability of the singular elements of a matrix (II)
For small enough
,
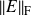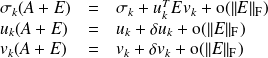
with
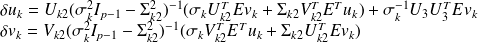
It is possible (chain rule) to find the Fréchet derivative
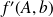of the truncated SVD solution using these formula
Condition number
Using the
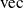operation,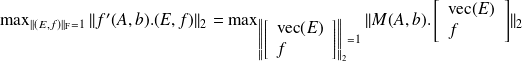
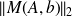represents the linear operator
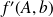for a particular basis of
The condition number
is
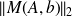
Sharp condition number estimate
Let
,
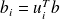Define
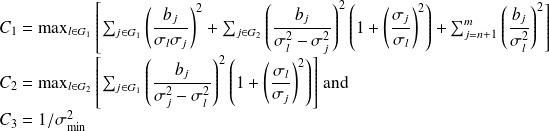
the quantity
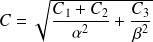is such that
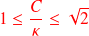
If
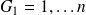, we get the least-squares condition number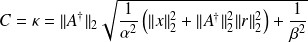
Numerical illustration
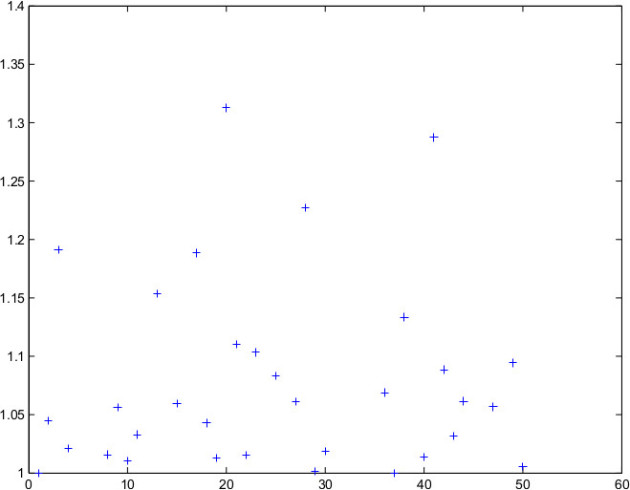
Verification
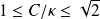for matrices of Matlab
Comparison with a results by P.C. Hansen
Take
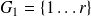
An absolute bound [Hansen, 98] gives to first order
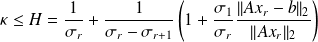
Take
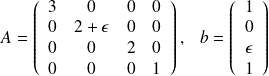
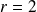then
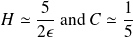for small
.
Conclusion
Adjoint formula for condition numbers in euclidean space may make the CN calculation easier
Relevance of partial condition number shown for test cases from parameter estimation
We can evaluate the sensitivity of
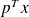where
is the solution of a (LLSP) when
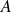and/or
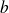are perturbedthe condition number in Frobenius norm can be computed via a close formula, a sharp estimate (factor
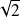) or a statistical estimate
The quantity to compute depends on the size of the problem (computational cost) and on the needed accuracy
The condition number in spectral norm can be estimated using a bound that lies within a factor 2
Pratical applications are planned in the area of geodesy
Sharp condition number obtained for the truncated SVD. Still efforts needed to apply this approach to large problem
