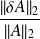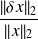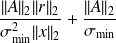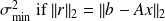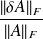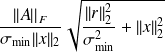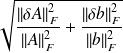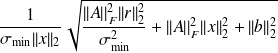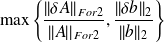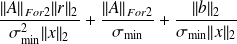The condition number(CN)
let
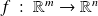 be Fréchet différentiable at
be Fréchet différentiable at
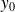
choose norms :
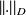 on
on
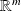 and
and
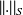 on
on
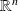
the condition number (CN) is [Rice, 66]
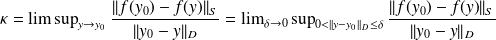
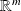 is the
is the dataspace and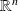 is the
is the solutionThe CN measures a first order sensitivity
Its order of magnitude is important for practical applications
Properties of condition numbers (CN)
the CN
 is a real positive number or
is a real positive number or
if
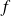 is lipschitz continuous around
is lipschitz continuous around
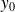 , with lipschitz constant
, with lipschitz constant
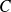 then
then
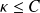
Examples
 for
for
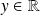 ,
,
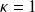 for
for
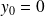 .
.For the polar factor
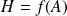 of
of
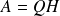 ,
,
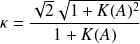
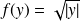 ,
,
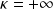 for
for
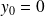
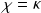 is the best possible constant such that
is the best possible constant such that
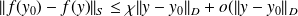
The condition numbers of a differentiable function
let
 be Fréchet différentiable at
be Fréchet différentiable at
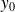
The norm
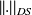 is the operator norm induced by
is the operator norm induced by
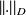 and
and
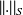
The condition number is
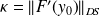
if i
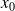 is implicitely defined by
is implicitely defined by
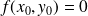 , and the asumption of the implicit function theorem hold at
, and the asumption of the implicit function theorem hold at
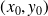 the condition number is
the condition number is
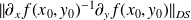
Practical questions : compute closed formula, sharp estimates or simply bound
Use of metrics
CN considered so far is the normwise absolute CN
If
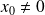 , the relative condition number is
, the relative condition number is
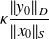
The term
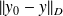 can be replaced in the limsup definition by the quantity
can be replaced in the limsup definition by the quantity
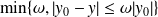 yielding a mixed condition number. Under the differentiability assumption, the absolute CN then
yielding a mixed condition number. Under the differentiability assumption, the absolute CN then
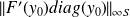 , the relative counterpart being
, the relative counterpart being
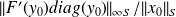
Product norms
In linear algebra the data space is often a cartesian product
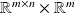
example
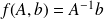 ,
,
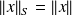 and
and
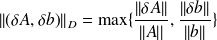 , where the matrix norm
, where the matrix norm
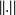 is induced by the vector norm ||{.}||. It is possible to show that
is induced by the vector norm ||{.}||. It is possible to show that 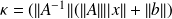
from
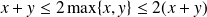 (
(
 ) follows that for
) follows that for
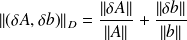 ,
, the CN
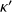 satisfies
satisfies
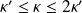 (
(
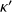 and
and
 have same order of magnitude).
have same order of magnitude).
Case of the linear least-squares problem
Source | Data | Solution | Formula | status | |
[ BJÖCK 96 ] |
|
|
| sharp | Dependence in
|
[ GEURST 82 ] |
|
|
| exact | Dependence in
|
[ GRATTON 96 ] |
|
|
| exact | Dependence in
|
[ GRCAR 04 ] |
|
|
| sharp | Dependence in
|
Why using the adjoint ?
differentiability assumption,
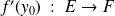 , condition number
, condition number
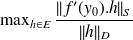
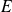 and
and
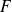 are finite dimension spaces. If
are finite dimension spaces. If
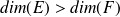 , it might be interesting to evaluate the CN using the adjoint of
, it might be interesting to evaluate the CN using the adjoint of

example : find the worse-case perturbation, or samples in a smaller space
aim of this part : show how duality results translate into CN estimation
Adjoints in a euclidean space
Let
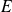 anf
anf
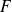 be two euclidean spaces
be two euclidean spacesThe scalar products norms and dual norms are denoted by
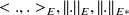 , i.e.
, i.e.
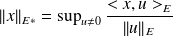 .
.the adjoint of the linear operator
 is defined by
is defined by
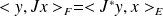 for any
for any
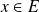 ,
,
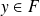
it is easily shown that
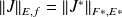
Composite norms
For the full rank least-squares problem,

Scalar products :
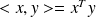 on
on
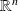 and
and
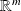 . The trace inner product is taken on
. The trace inner product is taken on
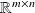 and
and
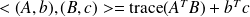 on the data space
on the data spaceWe denote by
 an absolute norm on
an absolute norm on
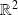 . Example
. Example
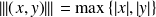
when
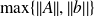 is considered. Let
is considered. Let
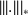 be its dual w.r.t. the canonical scalar product on
be its dual w.r.t. the canonical scalar product on
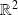 . Then the dual of
. Then the dual of
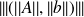 is
is
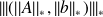 .
.
Case of the linear least-squares
For the least-squares,
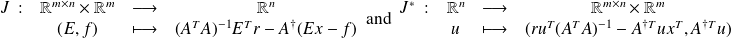
possible norm
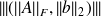 ; the adjoint is
; the adjoint is
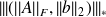
maximization over a vector space of dimension
 , instead of a maximization over a vector space of dimension
, instead of a maximization over a vector space of dimension
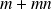
in next part, the operator norm is directly computed using statistical methods based on sampling