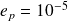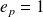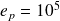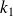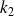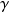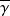Computation of a condition estimate
Statistical estimate
Let
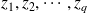be
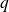orthonormal vectors uniformly and randomly selected in the unit sphere
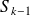in
dimensions (
)
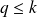and denote
.
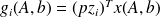Then
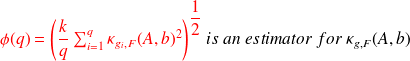
Demonstration
We have
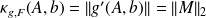
where
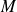is the
by
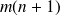matrix such that
.
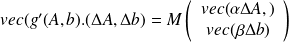[Kenney & Laub 94] supplies an estimator for
(
) and we obtain
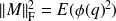
Estimate quality
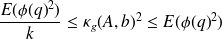
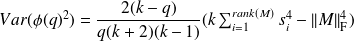where the
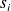are the nonzero singular values of
.
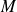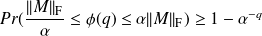when
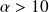
Then (adjoint), since
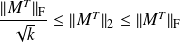
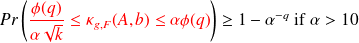
If
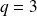, this probability reaches
.
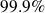Computation
Since
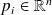, each
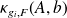is computed using
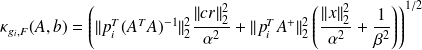
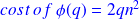
Remark on numerical reliability
Consider
a
Vandermonde matrix,
a random vector and
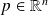the right singular vector
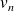
If the Cholesky factor of
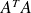has been obtained as the
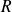factor of the
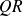decomposition of
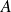, we get
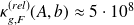. If
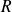is computed via a classical Cholesky factorization, we get
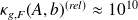. This is of pratical importance since the statistical estimate relies on an accurate computation of the
.
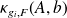Numerical experiments
Matrix family
We generate
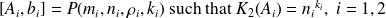Then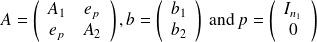
We compute on
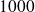random
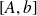
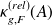using the SVD of
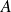
the statistical estimate
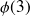
the ratio
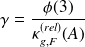
Asymptotic behaviour of the estimate
condition |
|
|
| ||||
|
|
|
|
|
|
|
|
1 | 1 | 1.22 | 0.23 | 1.15 | 0.30 | 1.07 | 0.36 |
1 | 8 | 1.02 | 0.32 | 1.22 | 0.31 | 1.21 | 0.34 |
8 | 1 | 0.90 | 0.30 | 1.13 | .030 | 1.06 | 0.35 |
8 | 8 | .092 | 0.29 | 1.22 | 0.30 | 1.18 | 0.33 |
Ratio between statistical and exact condition number of
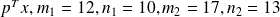mean and standard deviation
