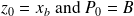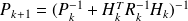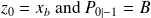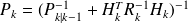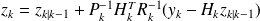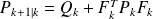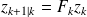Kalman filter
Optimality transfer for observations
We consider
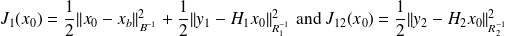 .
.We set
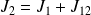
Is it possible to update de minimum argument
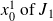 to get the minimum argument
to get the minimum argument
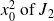 ?
?Application. Observations are obtained repeatly and we want to update the estimate accordingly, without processing all the information from the beginning.
Note that from Theorem(19), the minimum covariance matrix for the estimation of
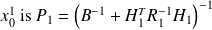 and
and
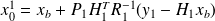
Fundamental : Theorem
For some constant
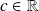 , we have
, we have
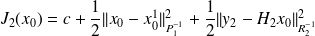 .
.
Therefore,
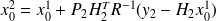 ,
,
where
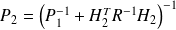 .
.
Proof
Since
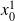 minimizes
minimizes
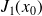 , we have the Taylor expansion
, we have the Taylor expansion
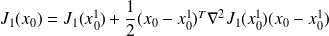 .
.
But
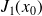 is quadratic, therefore,
is quadratic, therefore,
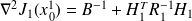 , and we have
, and we have
 , which yields the result.
, which yields the result.
This Theorem shows how to update incrementaly the estimation for new coming observations. Note that the algorithm updates the solution and the covariance matrix.
Incremental least squares algorithm
We want to find
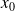 that minimizes
that minimizes
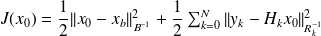 .
.
The following algorithm finishes with
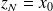 .
.
|
Note that this algorithm may be unstable in the presence of rounding-errors (on a computer) and that alternative formulations based on orthogonal transformations are available.
Optimality transfer for model errors
We consider
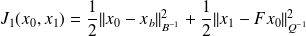 and
and
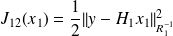 .
.We set
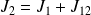 .
.Is it possible to update the minimum argument
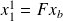 of
of
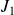 to get the minimum argument
to get the minimum argument
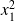 of
of
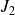 ?
?Application. Now we get observations from an object that is moving. The position of the object at
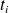 is
is
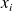 , and we would like to know the current position at
, and we would like to know the current position at
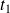 of the object "knowing" an approximate dynamics
of the object "knowing" an approximate dynamics
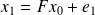 and noisy observations
and noisy observations
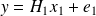 .
.
Fundamental : Theorem
For some constant
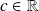 , some vector
, some vector
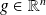 , and some matrix
, and some matrix
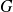 ,
,
we have
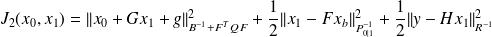 .
.
Therefore,
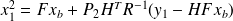 , where
, where
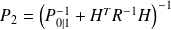 and
and
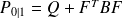 .
.
Proof
From bloc Gaussian elimination, we have
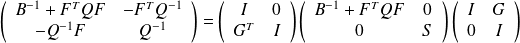 ,
,
where
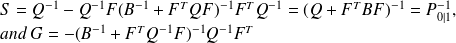 .
.
We have
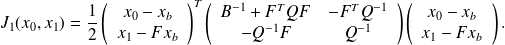
We denote
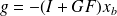 , and get
, and get
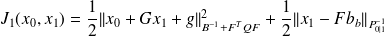 .
.
The conclusion follows from the fact that the minimum for
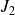 is obtained for
is obtained for
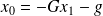 , and Theorem(19) provides an expression for
, and Theorem(19) provides an expression for
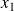 minimizing
minimizing
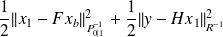 .
.
Kalman filter
We want to find
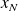 such that
such that
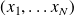 minimizes
minimizes
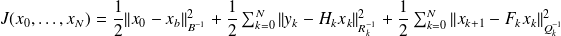 .
.
The following algorithm finishes with
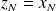 .
.
|
Again, algorithm may be unstable in the presence of rounding-errors (on a computer) an use orthogonal transformations recommended.