Steps in duality
Saddle point and augmented Lagrangian
Saddle point (SP) associated with a function
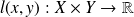 is a point
is a point
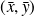 such that
such that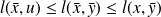 (SP1)
(SP1)An equivalent definition of a SP is
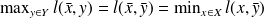 (SP2)
(SP2)For the minimization problem
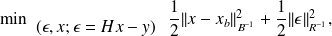
We consider the SP of the augmented Lagrangian associated with the optimization problem
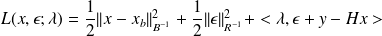
Convexity
For a convex differentiable function
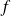 we consider the convex optimization problem
we consider the convex optimization problem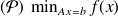
We have
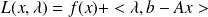
Theorem: The saddle points of
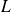 are exactly the points
are exactly the points
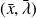 such that
such that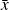 is a solution of
is a solution of
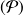 , and
, and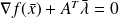 and
and
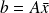
We consider the saddle point problem for the Lagrangian of the data assimilation problem.
From definition SP2, we introduce the direct problem
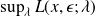 and the adjoint problem
and the adjoint problem
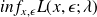 .
.
The direct problem
From
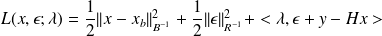
we get
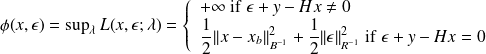
This yields the infsup result
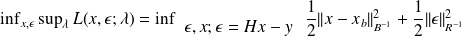
where the inf is a min by convexity.
Direct explicitation of the constraint leads to the problem
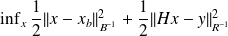
whose solution is given by the normal equations
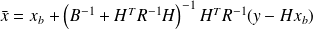 .
.
The adjoint problem
Consider the infimum problem
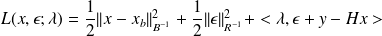
The problem is convex differentiable. Zeroing the partial derivative wrt
 and
and
 , we get
, we get
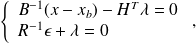
which yields
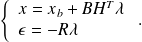
Keeping in mind SP2, we consider
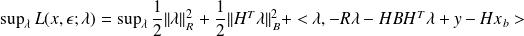
that leads to the adjoint maximization problem
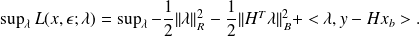
The solution is
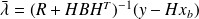 that yields
that yields
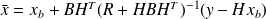 .
.
We see that the alternative formula obtained from the Sherman-Morrison formula can be obtained from duality theory.





