Solution algorithms
Newton method
Depends on the problem size. for reasonable size problems (machine?) it requires the solution of
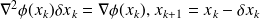
It converges locally quadratically to a critical point
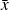 under some assumptions (
under some assumptions (
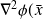 is Lipschitz continuous around
is Lipschitz continuous around
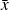 and
and
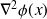 is SPD)
is SPD)It is possible to make the convergence global under mild assumptions with trust-region techniques. Linesearch is also possible.
If feasible (size, computational cost) this is a method of choice.
Impraticable for the ocean and atmosphere data assimilation problems.
Quasi-Newton Method
Several variantis available (SR1, PSB, DFP, BFGS,..)
For BFGS, the matrice
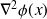 is not computed, but its inverse
is not computed, but its inverse
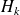 is approximated using the secant equation :
is approximated using the secant equation :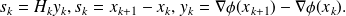
The matrix
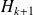 is the closest matrix to
is the closest matrix to
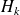 for some weighted norm
for some weighted normUpdating formula
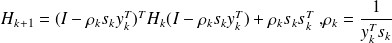
Limited memory implementation :
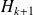 is kept in factored form and only the last pairs are taken into account
is kept in factored form and only the last pairs are taken into account
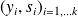 . Example : L-BFGS, M1QN3.
. Example : L-BFGS, M1QN3.
Quasi-Newton method for data assimilation
Gradient computation
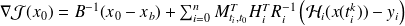 ,
,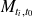 and
and
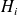 are the jacobian matrices of
are the jacobian matrices of
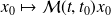 and
and
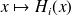 at
at
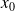 and at
and at
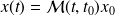
Computing, storing at all step
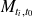 is not feasible in large scale data assimilation
is not feasible in large scale data assimilation
The Gauss-Newton algorithm
Solution of a sequence of linear least squares problems
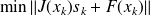 and update
and update
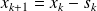
It can be seen as a stationary iteration
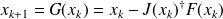
Does not require second order information. The linear least-squares problem can be solved by a direct or an iterative method (truncated Gauss-Newton method).
Local convergence of stationary iterations
Definition :
The process
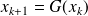 is locally convergent to
is locally convergent to
 , if there exist
, if there exist
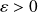 such that any sequence
such that any sequence
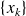 generated by (
generated by (
 ) converges to
) converges to
 whenever
whenever
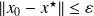 . In this case,
. In this case,
 is called a point of attraction.
is called a point of attraction.
If
 is a point of attraction of (
is a point of attraction of (
 ) and if
) and if
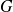 is continuous at
is continuous at
 , then
, then
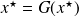 , that is,
, that is,
 is a fixed point of
is a fixed point of
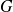
In the case where
 is a fixed point of
is a fixed point of
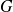 , but not a point of attraction of (
, but not a point of attraction of (
 ), the sequence
), the sequence
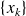 may behave in a variety of ways:
may behave in a variety of ways: it may diverge, cycle, or even exhibit a chaotic behaviour.
Ostrowsky's sufficient convergence condition
Let
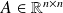 ,
,
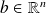 , and
, and
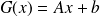 . We denote by
. We denote by
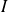 the identity matrix of order
the identity matrix of order
 .
.
It is well known that, if
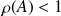 ,
,
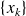 converges to
converges to
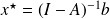 for any
for any
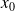 . In particular,
. In particular,
 is a point of attraction of (
is a point of attraction of (
 ).
).
Generalization of this result in the case where $G$ is no longer a linear mapping:
Fundamental : Theorem
Suppose that
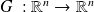 has a fixed point
has a fixed point
 , that
, that
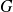 is Fréchet differentiable at
is Fréchet differentiable at
 , and that
, and that
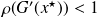 .
.
Then
 is a point of attraction of the iteration (
is a point of attraction of the iteration (
 ).
).
Asymptotic speed of convergence
Let
 be a fixed point of
be a fixed point of
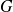 . Let
. Let
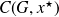 be the set of all of the sequences
be the set of all of the sequences
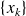 generated by (
generated by (
 ) and that converge to
) and that converge to
 .
.
Fundamental : Theorem
Suppose
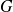 and
and
 satisfy the assumptions of Theorem
satisfy the assumptions of Theorem
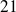 . For
. For
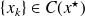 , one has
, one has
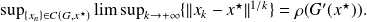
Moreover, for any
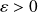 and
and
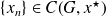 , there exists a norm
, there exists a norm
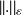 such that
such that
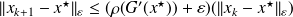 for k large enough.
for k large enough.
Remarks on Ostrowsky Theorem
he quantity
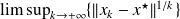 is referred to as the root convergence factor of the sequence
is referred to as the root convergence factor of the sequence
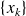 ,
,converging to
 . It can be shown (Ortega, Rheinboldt) that the root convergence factor does not depend on the norm chosen on
. It can be shown (Ortega, Rheinboldt) that the root convergence factor does not depend on the norm chosen on
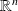 .
.Theorem (
 ) shows that, if
) shows that, if
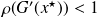 , for any sequence
, for any sequence
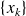 generated by (
generated by (
 )
) that converges to
 and for any
and for any
 such that
such that
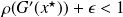 , there exists
, there exists
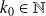 such that
such that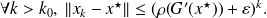
Therefore, the convergence of
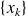 is as rapid as a geometric progression of rate
is as rapid as a geometric progression of rate
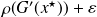 .
.Using the norm
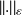 of Theorem (
of Theorem (
 ) , there exists
) , there exists
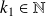 such that
such that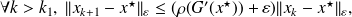 that is,
that is,
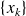 converge linearly to
converge linearly to
 .
.Using Theorem (
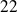 ), for
), for
 large enough, the smaller
large enough, the smaller
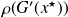 , the faster the error
, the faster the error
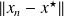 decreases as
decreases as
 increases.
increases.Therefore, if
 and
and
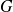 satisfy the assumptions of Theorem (
satisfy the assumptions of Theorem (
 ), the quantity
), the quantity
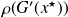
can be used to measure the asymptotic speed of the convergence of the stationary iteration
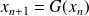 .
.
Local convergence and linear rate of convergence
We denote by
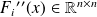 the Hessian matrix of the function
the Hessian matrix of the function
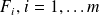 .
.
Let
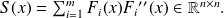
We define
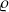 by
by
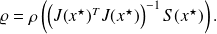
Obviously,
 is a fixed point of
is a fixed point of
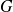 if
if
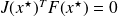 .
.
The following theorem of local convergence holds :
Fundamental : Theorem
If
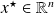 is a fixed point of
is a fixed point of
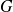 ,
,
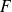 is twice continuously Fréchet differentiable in a neighborhood
is twice continuously Fréchet differentiable in a neighborhood
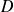 of
of
 ,
,
and that
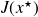 has full rank
has full rank
 . If
. If
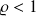 , then the Gauss-Newton iteration converges locally to
, then the Gauss-Newton iteration converges locally to
 .
.
Proof
A direct computation of
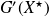 reveals that
reveals that
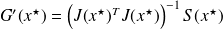 .
.
Let us denote by
 the surface in
the surface in
 given by the parametric representation
given by the parametric representation
 .
.
The fixed point condition
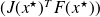 has the geometrical interpretation that follows.
has the geometrical interpretation that follows.
let
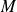 be the point of
be the point of
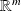 of coordinates
of coordinates
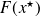 and
and
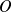 the origin of the coordinate system.
the origin of the coordinate system.
The vector
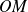 is orthogonal to the plane tangent through
is orthogonal to the plane tangent through
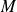 to the surface
to the surface
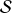 .
.
Fundamental : Theorem
Suppose that the assumptions of the previous Theorem hold and
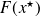 is nonzero.
is nonzero.
One has
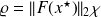 ,
,
where
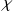 is the maximal principal curvature of the surface ${\cal{S}}$ at point
is the maximal principal curvature of the surface ${\cal{S}}$ at point
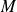 with respect to the normal direction
with respect to the normal direction
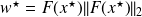 .
.
Proof
We consider a curve
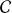 through
through
 on the surface given by the parametric representation
on the surface given by the parametric representation
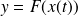 , and let
, and let
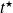 be such that
be such that
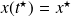 . The intrinsic parameter
. The intrinsic parameter
 on the curve
on the curve
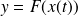 satisfies
satisfies
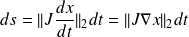 ,
,
where
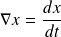 . The curvature vector of the curve at
. The curvature vector of the curve at
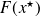 is by definition
is by definition
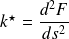 . Using the chain rule, yields
. Using the chain rule, yields
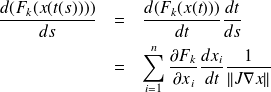
Again, the chain rule enables to obtain
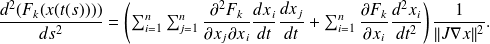
The maximal principal curvature of the surface
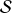 at point
at point
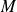 with respect to the normal direction
with respect to the normal direction
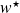 is by definition the supremum over all the curves on
is by definition the supremum over all the curves on
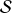 passing through
passing through
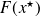 of the scalar product
of the scalar product
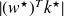 .
.
Since
 is a fixed point of the iterations,
is a fixed point of the iterations,
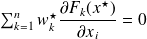 , therefore,
, therefore,
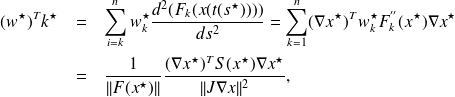
were we have denoted by
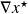 the quantity
the quantity
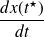 . The searched supremum is
. The searched supremum is
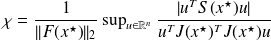
and matrix manipulations show that this quantity is equal to

Local convergence properties of the Gauss-Newton algorithm
The algorithm is not globally convergent. It is not locally convergent either : for some problems, a fixed point may be a repelling fixed point.
Consider
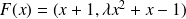 .
.The unique local minimum is
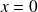 .
.It is possible to show that
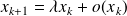 .
.Therefore, if
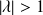 ,
,
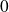 is a repelling fixed point.
is a repelling fixed point.
Example of nonlocal convergence of Gauss-Newton
The incremental 4D Var algorithm (Gauss-Newton)
Take
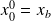
For {
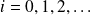 } solve iteratively the quadratic minimization problem
} solve iteratively the quadratic minimization problem
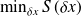 , with
, with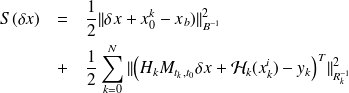
Update
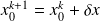
End for
where we set
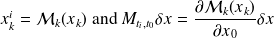 .
.





