The problem
A nonlinear least squares problem
We define
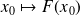by
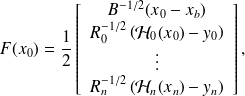
then the minimization of the 4D Var functional reads
This is an unconstrained nonlinear least-squaresproblem.
Let
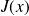be the Jacobian matrix of
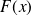and, whenever
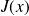is differentiable, let
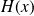be the Hessian matrix of
.
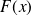Existence and unicity of solutions
Differentibility of
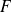assumed.If
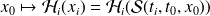(or if
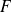) is an affine function of
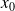the optimization problem is a full rank overdeterminedlinear least squares problem. The solution correspondsto a linear system of equations (the normal equations).
If the problem is non linear then existence and unicity are not guaranteed in general. An iterative algorithm
has to be used in general.
Derivatives for the nonlinear least squares functional
Let
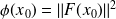
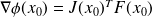
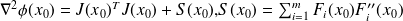
The necessary condition for optimality
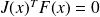. A point that satisfies this condition is a (first order) critical point.
Geometrical interpretation
Minimum distance from the origin to the surface de
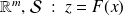
For a critical point
such that
,
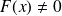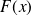orthogonal to Im
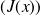and, if
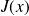has full column rank,The matrix
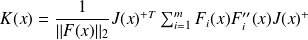is the principal curvature matrix associated to
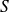wrt the normal direction
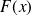
Let
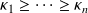be the eigenvalues of
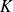. The quantites
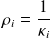are the principal curvature radii wrt to the normal direction
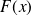
We then have
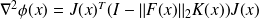
Critical points and extrema
Let
be a critical point, and assume
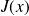has full colummn rank and
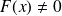
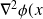) is symmetric positive definite if
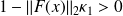. Then
is a local minimum of
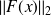. This is the second order sufficient optimality condition.
If
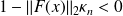, then
is a local maximum of
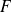
If
is a local min, then
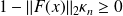. This is the
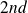order necessary condition of optimality.A nonlinear least squares problem may have
no local minimum (ex:
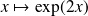)many local minima (ex:
)
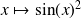