Opérations sur les limites
![]() désigne un réel fini,
désigne un réel fini, ![]() ou
ou ![]() .
.
Fondamental :
Soient ![]() et
et ![]() deux fonctions qui admettent respectivement
deux fonctions qui admettent respectivement ![]() et
et ![]() (finies) lorsque
(finies) lorsque ![]() tend vers
tend vers ![]() , alors
, alors
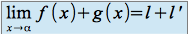
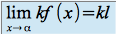 quelque soit
quelque soit 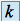 réel
réel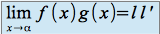
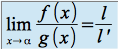 si
si 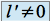
Fondamental :
Si ![]() et
et ![]() alors :
alors :
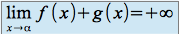
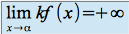 si
si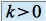 et
et 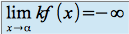 si
si 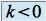
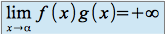
Fondamental :
Si ![]() (
(![]() réel fini) et
réel fini) et ![]() alors :
alors :
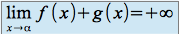
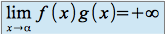 si
si 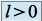 et
et 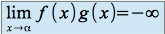 si
si 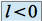
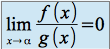 si
si 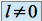
Fondamental :
![]() est un réel fini,
est un réel fini,
Si
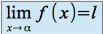 et
et 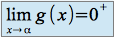 alors
alors 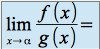 (signe de
(signe de 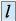 )
)
Si
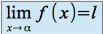 et
et 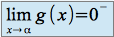 alors
alors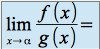 (signe de
(signe de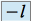 )
) 
Remarque :
Il existe plusieurs cas, appelés formes indéterminées :
Si
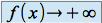 et
et 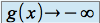 , on ne peut pas conclure immédiatement pour la limite de
, on ne peut pas conclure immédiatement pour la limite de 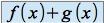
Si
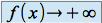 (ou
(ou  ) et
) et 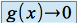 , on ne peut pas conclure immédiatement pour la la limite de
, on ne peut pas conclure immédiatement pour la la limite de 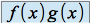
Si
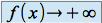 (ou
(ou  ) et
) et 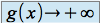 (ou
(ou  ), on ne peut pas conclure immédiatement pour la limite de
), on ne peut pas conclure immédiatement pour la limite de 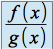
Si
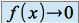 et
et 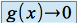 , on ne peut pas conclure immédiatement pour pour la limite de
, on ne peut pas conclure immédiatement pour pour la limite de 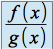
Exemple :
Soit ![]() et
et ![]() .
.
Déterminer ![]()
On ne peut conclure directement, on est en présence d'une forme indéterminée![]()
![]() .
.
On écrit : ![]()
Donc ![]() , car
, car ![]()
Et donc ![]()





