Limite réelle (finie) en a
Définition :
est une fonction définie sur 
sauf peut-être au point 
. Dire que 
tend vers 
lorsque 
tend vers signifie que tout voisinage de contient toutes les valeurs de pour assez voisin de .
On écrit : 
ou
Autrement dit :
Remarque :
si est définie en et si la limite de existe alors 
.
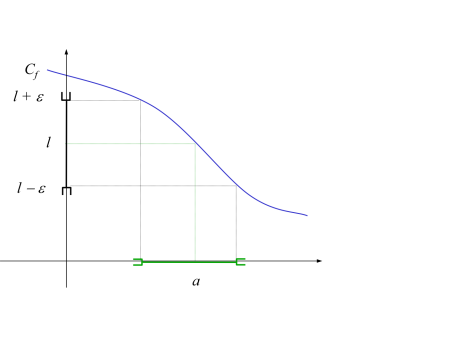
Limite réelle en a
Exemple :
Chercher la limite en 
de 
définie sur 
On a : 
donc, pour 
, on a : 
et 
donc 
on en déduit :
Exemple :
Soit la fonction définie sur 
par : 
, mais 
n'est pas la limite de en 1, en effet l'intervalle 
, contenant ne contient pas toutes les valeurs de pour voisin de 
: 
et 
