Applications des développements limités
Applications des développements limités
Soit la fonction ![]() , définie sur
, définie sur ![]() par :
par : ![]()
Question
Donner un développement limité à l'ordre de
 de
de 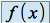 en
en 
En déduire une équation de la tangente
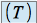 à
à 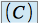 au point d'abscisse
au point d'abscisse 
Etudier la position de
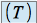 par rapport à
par rapport à 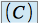 au voisinage de ce point.
au voisinage de ce point.
Donnons le développement limité à l'ordre de
 de
de 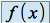 en
en  .
.On calcule :
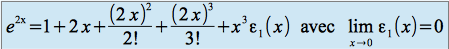
puis
soit
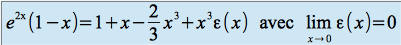
Et donc :
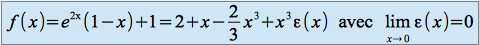
L'équation de la tangente
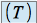 à
à 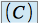 est donnée par les deux premiers termes du
est donnée par les deux premiers termes du 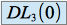 précédent (cf formule de Taylor,
précédent (cf formule de Taylor,  étant infiniment différentiable) :
étant infiniment différentiable) :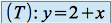
Au voisinage de
 , on a :
, on a :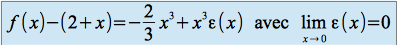
Pour
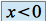 ,
, 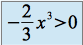 et
et  . Donc
. Donc 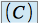 est au dessus de
est au dessus de 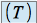 .
.Pour
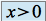 ,
, 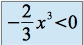 et
et 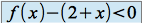 . Donc
. Donc  est en dessous de
est en dessous de  .
.





