Continuité, dérivabilité
Continuité, dérivabilité
On considère la fonction 
définie sur
par :
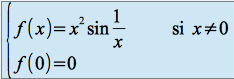
Question
Etudier la continuité et la dérivabilité de
Solution
D'une part
est continue sur 
d'après les théorèmes généraux.D'autre part on peut écrire
On en déduit
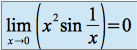
Donc
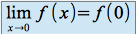et est continue en 
Ainsi
est continue sur
D'après les théorèmes généraux,
est dérivable en tout point de .D'autre part
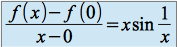
On écrit :
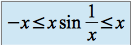
On en déduit
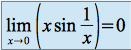
Donc
est dérivable en et 
Ainsi
est dérivable sur et :
