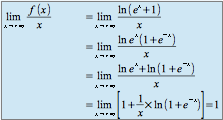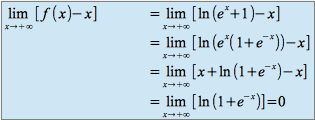Fonctions logarithme et exponentielle
Fonctions logarithme et exponentielle
.
Question
Etudier les variations de la fonction 
. On vérifiera que lorsque 
tend vers
, la courbe représentative de 
est asymptote à la droite d'équation
. Montrer que cette fonction admet une réciproque 
et expliciter cette dernière.
D'après les théorèmes généraux, est définie et dérivable sur 
On a : 
,
, est donc continue et strictement croissante sur
On a : 
donc 
De même : 
donc
La droite d'équation : 
est asymptote à la courbe.
On a :
De même :
La droite d'équation : est donc asymptote à la courbe représentative de .
est continue et strictement croissante sur , est donc une bijection de sur 
Donc est une bijection de sur
Soit 
Notons que si 
, alors 
.
Donc :
