Accroissements finis
Accroissements finis
.
Question
Montrer que pour tout
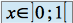
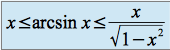
En déduire
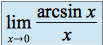
Soit
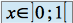. On appelle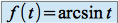
est dérivable sur 
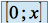
D'après le théorème des accroissements finis, il existe un réel
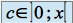tel que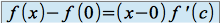 
Donc
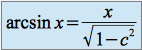
Or
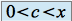
donc
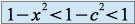
donc
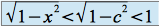(on sait que
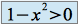)et donc
(passage à l'inverse).On en déduit :
(multiplication par
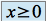)Finalement :
(1)
On déduit de ce qui précède :
Donc
Ajoutons que :
(d'après (1))Donc
(car est impaire)Et donc
On en déduit :
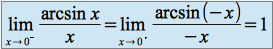
Les limites à gauche et à droite en
sont égales, on en déduit que : 
