Equation différentielle du second ordre
Equation différentielle du second ordre
Question
Déterminer la forme générale de la solution de l'équation différentielle ![]() :
:
![]()
![]()
L'équation ![]() peut s'écrire :
peut s'écrire :
![]()
C'est une équation différentielle du second ordre à coefficients constants. On résout l'équation homogène, puis on recherchera une solution particulière.
Solution de l'équation homogène : on suppose une solution du type
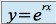 , ce qui conduit à l'équation caractéristique :
, ce qui conduit à l'équation caractéristique :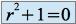
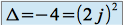
Cette équation admet deux racines complexes conjuguées :
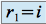 et
et  . La solution est donc :
. La solution est donc :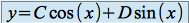
où
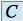 et
et 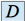 sont des constantes réelles.
sont des constantes réelles.Solution particulière : le second membre est une combinaison linéaire de fonctions de la forme
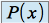 , polynôme de degré
, polynôme de degré  et d'une fonction trigonométrique. On recherchera donc une solution particulière du type
et d'une fonction trigonométrique. On recherchera donc une solution particulière du type  , soit :
, soit :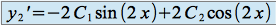

En injectant ces relations dans l'équation
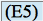 , nous obtenons :
, nous obtenons :Soit
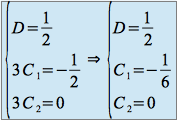
On obtient donc la solution particulière :
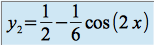
La solution générale de l'équation ![]() est donc :
est donc : ![]()
où ![]() et
et ![]() sont des constantes réelles.
sont des constantes réelles.





