Equation différentielle du premier ordre
Equation différentielle du premier ordre
Question
Déterminer la forme générale de la solution de l'équation différentielle 
:
avec la condition : 
C'est une équation différentielle du premier ordre à coefficients non constants du type
On résout l'équation homogène, puis on recherchera une solution particulière.
Solution de l'équation homogène :
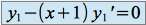
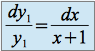
Les variables sont séparées, on intègre séparément les membres de droite et gauche.
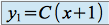
où
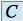est une constante réelle.Solution particulière : on applique la méthode de la variation de la constante. On suppose donc que :
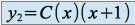
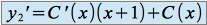
En injectant ces relations dans l'équation
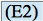, nous obtenons :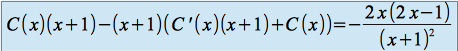
d'où
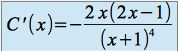
La décomposition en éléments simples du membre de droite conduit à :
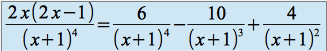
D'où :
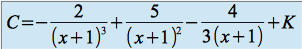
et la solution particulière recherchée (prise pour
) :
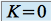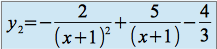
La solution générale de l'équation est donc :
où est une constante réelle.
