Equation différentielle du second ordre
Equation différentielle du second ordre
Question
Déterminer la forme générale de la solution de l'équation différentielle 
:
C'est une équation différentielle du second ordre à coefficients constants. On résout l'équation homogène, puis on recherchera une solution particulière.
Solution de l'équation homogène : l'équation caractéristique est :
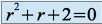
Cette équation a deux racines complexes :
La solution s'écrit :
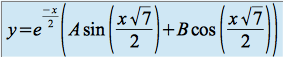
et 
ét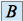ant deux réels quelconques.Solution particulière : cherchons une solution particulière sous la forme :
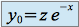de l'équation différentielle 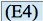. En reportant dans l'équation, on obtient :
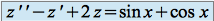
Enfin une solution de l'équation
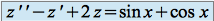est recherchée sous la forme
en reportant dans l'équation 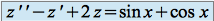, on obtient 
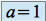et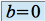 
La solution générale de l'équation est donc :
et étant deux réels quelconques.
