Prolongement par continuité
Définition : Prolongement continu
Si 
est une fonction définie sur un intervalle 
contenant le réel 
, sauf en , et si 
la fonction 
définie par: 
s'appelle prolongement continu de .
Exemple :
Soit définie par :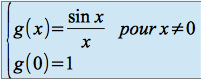 
est le prolongement continu de la fonction définie sur 
par : 
