Continuité en un point, sur un intervalle.
Définition : fonction continue au point a
est une fonction définie sur un intervalle 
ouvert contenant 
. On dit que est continue en si et seulement si : 
.
Autrement dit :
Fondamental : Théorème
Soient et 
deux fonctions continues en , alors 
, 
et 
sont continues en . De plus, si 
alors 
est continue en .
Définition :
Soient , 
deux intervalles de 
, 
, 
telles que 
. On note :
Fondamental : Théorème
Soient une fonction continue en et une fonction continue en 
, alors la fonction 
est continue en .
Définition : Continuité sur un intervalle
On dit que
est continue sur l'intervalle 
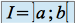si et seulement si est continue en tout point de .On dit que
est continue sur l'intervalle 
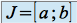si et seulement si est continue sur 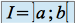, continue à droite en et continue à gauche en 
.
Remarque :
dire que
est continue à droite en signifie que :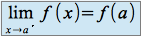 
Graphiquement, la continuité d'une fonction
sur un intervalle correspond au fait que l'on peut tracer la représentation graphique de sur
d'un trait de crayon continu.)
Contre exemple: Soit la fonction définie sur par : 
n'est pas continue sur , car 
et 
, n'a donc pas de limite en 1, et donc n'est pas continue au point 1.
