Définitions et propriétés
Introduction
La compatibilité intrinsèque des applications linéaires avec la notion de combinaison linéaire, fait que :
L'image d'un s.e.v par une application linéaire est un espace vectoriel.
L'image réciproque d'un s.e.v par une application linéaire est aussi un espace vectoriel.
En particulier, on définit des sous espaces vectoriels très importants pour la suite :
Définition : Noyau et image d'une application linéaire
Soit 
une application linéaire d'un espace vectoriel 
dans un espace vectoriel 
.
Le noyau de
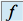, noté 
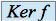, est l'ensemble des vecteurs de 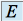dont l'image par 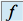est le vecteur nul de ,
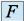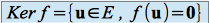.L'image de
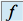, notée 
, est l'ensemble des images dans 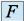des vecteurs de 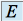par l'application ,
.
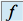Une application utile : On détermine souvent pour savoir si l'application linéaire est ou non injective. En effet, on a le résultat suivant :
Fondamental : Théorème
Soit une application linéaire. On a l'équivalence suivante :
