Approche de la notion d'espace vectoriel
Introduction
Vous connaissez l'ensemble
des vecteurs de 
. Sur
on peut définir plusieurs opérations :
L'addition de deux vecteurs
Rappel :
,
qui est une loi interne dans
. On dit que cette loi est interne car, à partir de deux vecteurs de
on construit un nouveau vecteur de
.
On vérifie aisément que cette loi interne est commutative (C), associative (A), que
est élément neutre pour cette loi
(N)
et que tout élément
deadmet un élément symétrique 
(S).
On conclut que
est un groupe commutatif.
La multiplication d'un vecteur par un nombre réel
.
Attention :
Cette loi n'est pas appelée loi interne car ce n'est pas à partir de deux vecteurs que l'on construit un nouveau vecteur, mais à l'aide d'un réel et d'un vecteur.
On dit que c'est une loi externe.
Cette multiplication possède les propriétés suivantes. Quels que soient les réels
et
, quels que soient les vecteurs
et
, on a :
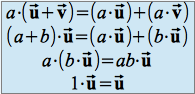
On dit quemuni de la loi interne
et de la loi externe
sur
est un espace vectoriel sur le corps. En résumé, 
est un-espace vectoriel.
