Exploitation concrète sur un exemple
Méthode :
Reprenons l'exemple traité au début du chapitre consacré aux matrices de l'application linéaire 
de 
dans 
, de matrice
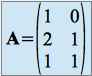
exprimée dans les bases canoniques 
de et 
de .
Le but de cet exemple était de déterminer l'expression matricielle 
de l'application dans deux nouvelles bases,
de , et 
de
dont les coordonnées sont exprimées dans les bases canoniques respectives.
Pour ce faire, il suffit d'exprimer les coordonnées de 
et 
dans la base 
, et de les "ranger'' en colonne dans la matrice .
On considère tout d'abord la matrice de passage de la base à la base 
:
déjà introduite dans l'exemple précédent. Les colonnes de la matrice 
étant égales aux coordonnées des vecteurs colonnes 
et 
exprimés dans la base , le produit
nous donne directement sous forme matricielle l'expression des vecteurs et dans la base à la base :
En reprenant la même démarche que celle détaillée dans l'exemple du début, on comprend que la matrice
représente l'endomorphisme identique de muni de la base dans muni de la base .
Finalement, le produit
nous donne le résultat recherché, c'est à dire en colonne l'expression de et dans la base .
