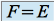Théorèmes fondamentaux
Fondamental : Théorème
Soit 
un espace vectoriel non réduit au vecteur nul, alors :
De toute famille génératrice on peut extraire une base
Toute famille libre de
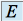peut être complétée de manière à former une base. (Théorème dit "de la base incomplète")
Fondamental : Théorème
Dans un espace vectoriel de dimension n, toute famille de plus de n éléments est liée.
Dans un espace vectoriel de dimension n, toute famille de moins de n éléments ne peut être génératrice.
Fondamental : Théorème
Soit un espace vectoriel de dimension n, alors :
Toute famille génératrice de n éléments est une base.
Toute famille libre de n éléments est une base.
Fondamental : Théorème
Soit un espace vectoriel de dimension finie et 
un sous espace vectoriel de , alors :
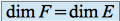si et seulement si 
