Définitions
Définition : Espaces vectoriels de dimension finie
On dira qu'un espace vectoriel 
sur le corps 
est de dimension finie, s'il admet une famille génératrice ayant un nombre fini d'éléments.
Définition : Base d'un espace vectoriel de dimension finie
Soit un espace vectoriel de dimension finie. On appelle base de toute famille finie de vecteurs 
libre et génératrice dans.
Attention :
Une telle famille n'est pas unique. Par contre, quand elles existent, toutes les bases d'un même espace vectoriel possèdent le même nombre de vecteurs. Ce nombre est appelé dimension de l'espace vectoriel
.
Remarque :
La notion de dimension est liée au corps sur lequel est construit l'espace vectoriel :
L'espace vectoriel
sur le corps 
est de dimension 2, une base de cet espace étant, par exemple,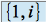 
.L'espace vectoriel
sur le corps est de dimension 1, et une base en est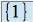 
.
Exemple :
Soit 
. 
est un s.e.v. de 
.
Soit 
. On a donc : 
. Ainsi, tout élément 
s'écrit :
.
On a montré que les vecteurs 
et 
forment une famille génératrice de , et (trivialement) libre dans.
La famille 
est donc une base de l'espace vectoriel , qui est par conséquent de dimension 2.
