III.3 Caractéristique statique [La jonction PN et ses applications]

III.3 Caractéristique statique

a) Cas général

Dans ce qui précède, nous venons de montrer que, lorsqu'on polarise une diode, on génère un excès de densité de porteurs. Il existe donc un gradient de concentration et par conséquence, il y aura diffusion de porteurs. La loi de répartition des porteurs en excès sera donnée par la solution de l'équation de conservation appliquée au cas particulier de la diode.

Cette équation s'écrit, dans le cas général, pour les trous dans la région neutre N : $\frac{d \hat{p}}{dt} = - \frac{1}{q} div \vec{j_{p}} + g_{p} - r_{p}$ .

Remarque :

On obtient la même équation pour les électrons dans la région neutre P en remplaçant $p$ par $n$ .

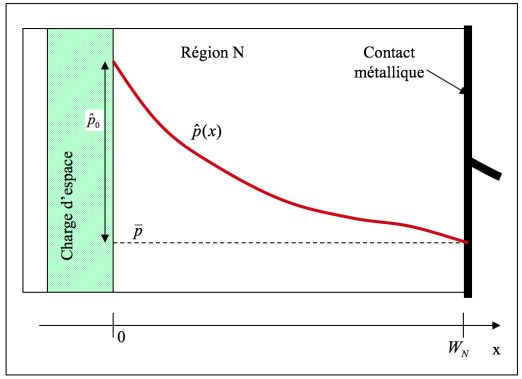
Nous allons étudier la solution de cette équation dans le cas de la diode représentée ci-dessus. Pour ce, nous considérerons simplement la diffusion des trous dans la région N (hypothèse de faible niveau d'injection). La contribution des électrons dans la région P pourra se déduire directement de ces calculs.

Pour pouvoir traiter cette équation, il faut connaître les conditions correspondant à notre dispositif.

La première constatation qui s'impose est que la génération se situe exclusivement dans le plan $x = 0$ . Il n'y a donc pas de génération en volume et de ce fait le terme $g_{p}$ de l'équation de conservation est nul.

La deuxième constatation est que, toute la tension appliquée se retrouvant aux bornes de la charge d'espace, la région N dans laquelle diffusent les porteurs est équipotentielle. Il n'y a donc pas de champ électrique dans cette zone ce qui implique que le courant est essentiellement dû à la diffusion.

Tout ceci permet de simplifier l'équation de conservation qui se réduit à : $\frac{d \hat{p}}{dt} = - \frac{1}{q} div \vec{j_{p}} - r_{p}$ .

En régime de faible injection : $r_{P} = \frac{\hat{p}}{τ_{P}}$

Le courant étant exclusivement dû à la diffusion, l'équation s'écrit : $\frac{\partial \hat{p}}{\partial t} = - \frac{1}{q} div (- q D_{P} \vec{grad} \hat{p}) - \frac{\hat{p}}{τ_{p}}$ .

Nous allons étudier cette équation en régime permanent ce qui implique : $\frac{\partial p}{\partial t} = 0$ .

Le cas du modèle unidimensionnel entraîne que les dérivations se font exclusivement suivant l'axe des $x$ . Il s'en suit : $D_{p} \frac{d^{2} p}{d x^{2}} - \frac{\hat{p}}{τ_{p}} = 0$ .

Il suffit donc de connaître les conditions aux limites en 0 et en $W$ pour obtenir la solution de cette équation. Elles s'écrivent :

en x = 0 : {\hat{p}}_{0} = \hat{p} (0) = \bar{p} \exp (\frac{V}{U_{T}} - 1)

en x = W_{N} : \hat{p} (W_{N}) = 0

En effet, quelle que soit la distance $W$ , le contact ohmique impose un excès de densité nul.

En écrivant : $\frac{d^{2} \hat{p}}{{dx}^{2}} - \frac{\hat{p}}{D_{p} τ_{p}} = 0 \Rightarrow \frac{d^{2} \hat{p}}{{dx}^{2}} - \frac{\hat{p}}{L_{p}} = 0$ ,

On montre que la solution de cette équation différentielle est (voir démonstration) : $\hat{p} (x) = \hat{p_{0}} \frac{sh (\frac{W_{N} - x}{L_{p}})}{sh (\frac{W_{N}}{L_{p}})}$

d'où:

J_{\hat{p}} (x) = - q D_{p} \frac{d}{dx} [{\hat{p}}_{0} \frac{sh (\frac{W_{N} - x}{L_{p}})}{sh (\frac{W_{N}}{L_{p}})}] = \frac{q D_{p} {\hat{p}}_{0}}{L_{p} sh (\frac{W_{P}}{L_{p}})} ch (\frac{W_{N} - x}{L_{p}})

Remarque :

Un calcul identique pour les électrons donne :

J_{\hat{n}} (x) = \frac{q D_{n} {\hat{n}}_{0}}{L_{n} sh (\frac{W_{P}}{L_{n}})} ch (\frac{W_{P} - x}{L_{n}})

Attention :

Si on suppose que la zce^[1] n'est le siège d'aucune génération-recombinaison, on peut considérer que le courant d'électrons et de trous est respectivement de même valeur de part et d'autre de la zce^[1].

On peut donc calculer le courant d'électrons et de trous en un « même » point $x = 0$ .

Le courant total, qui est conservatif, c'est-à-dire indépendant de $x$ est alors :

\begin{matrix} I & = & A_{J} [J_{\hat{p}} (0) + J_{\hat{n}} (0)] = A_{J} [\frac{q D_{n} {\hat{n}}_{0}}{L_{n} sh (\frac{W_{P}}{L_{n}})} ch (\frac{W_{P}}{L_{n}}) + \frac{q D_{p} {\hat{p}}_{0}}{L_{p} sh (\frac{W_{N}}{L_{p}})} ch (\frac{W_{N}}{L_{p}})] \\ \Rightarrow I & = & q A_{J} [\frac{D_{n} {\hat{n}}_{0}}{L_{n} th (\frac{W_{P}}{L_{n}})} + \frac{D_{p} {\hat{p}}_{0}}{L_{p} th (\frac{W_{N}}{L_{p}})}] \end{matrix}

Or ${\hat{n}}_{0} = \bar{n} [\exp (\frac{V}{U_{T}}) - 1] = \frac{n_{i}^{2}}{N_{A}} [\exp (\frac{V}{U_{T}}) - 1]$ et ${\hat{p}}_{0} = \bar{p} [\exp (\frac{V}{U_{T}}) - 1] = \frac{n_{i}^{2}}{N_{D}} [\exp (\frac{V}{U_{T}}) - 1]$ .

Donc:

Fondamental :

I = q A_{J} n_{i}^{2} [\frac{D_{n}}{N_{A} L_{n} th (\frac{W_{P}}{L_{n}})} + \frac{D_{p}}{N_{D} L_{p} th (\frac{W_{N}}{L_{p}})}] [\exp (\frac{V}{U_{T}}) - 1]

Cette expression fait apparaître deux termes:

- une constante qui ne dépend que des caractéristiques géométriques et des dopages,

- un terme qui fait apparaître la tension de polarisation.

Définition :

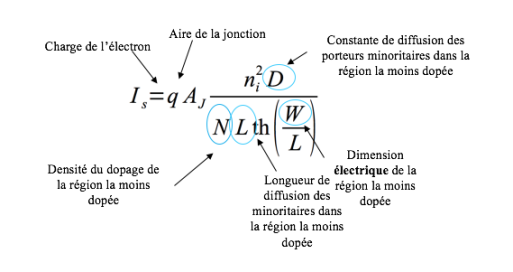
Le terme constant est appelé courant inverse théorique. Il a pour expression:

I_{s} = q A_{J} n_{i}^{2} [\frac{D_{n}}{N_{A} L_{n} th (\frac{W_{P}}{L_{n}})} + \frac{D_{p}}{N_{D} L_{p} th (\frac{W_{N}}{L_{p}})}]

Définition :

L'expression du courant d'une diode peut donc se mettre sous la forme :

I = I_{s} [\exp (\frac{V}{U_{T}}) - 1]

b) Jonction dissymétrique

Définition :

Une jonction est dite dissymétrique si les densités de dopage des 2 côtés de la jonction diffèrent d'au moins un facteur 100.

Remarque :

L'expression du courant inverse théorique fait apparaître deux termes correspondant aux courants de diffusion des porteurs minoritaires dans chacune des régions. Chacun de ces termes est inversement proportionnel à la densité des porteurs majoritaires de la région correspondante.

Conseil :

Si la jonction est franchement dissymétrique, le courant correspondant à cette dernière sera très petit et pourra être négligé:

Tout se passe alors comme si seule la région la moins dopée intervenait.

Fondamental :

Ainsi, pour une jonction P⁺ N, le courant sera essentiellement un courant de trous qui dépendra des caractéristiques de la région N.

L'unidirectionnalité de la jonction sera matérialisée par le rendement d'injection : $γ_{E} = \frac{I_{S_{N}}}{I_{S_{N}} + I_{S_{P}}}$ (pour une diode N+P).

Remarque :

Il suffira d'inverser les indices relatifs à la région ou aux porteurs pour obtenir le cas N⁺ P.

Remarque :

Ainsi, dans le cas d'une jonction dissymétrique, le courant inverse théorique se réduira à :

c) Cas particulier de la diode courte

Méthode :

Lorsque les dimensions des régions son petites vis-à-vis des longueurs de diffusion, on peut simplifier les expressions.

En effet les termes en $W / L$ interviennent sous forme de tangentes hyperboliques qui, pour des faibles valeurs de l'argument, peuvent se linéariser :

pour $ϵ ≪ 1$ , $th ϵ \to ϵ$ . Par exemple, pour $th (1 / 3) = 0,339$ , soit sensiblement $1 / 3$ . On a alors $L th (\frac{W}{L}) \to W$ .

L'expression du courant inverse théorique s'écrit dans le cas d'une possible simplification : $I_{s} = q A_{J} n_{i}^{2} (\frac{D_{n}}{N_{A} W_{P}} + \frac{D_{p}}{N_{D} W_{N}})$ .

On considérera donc que, si cette condition est vérifiée, les équations vont se simplifier. Ce cas sera celui que l'on rencontrera généralement.

Remarque :

On pourra remarquer que, dans ce cas, les différentes équations qui ont été établies sont linéarisées. La distribution des porteurs suivra une loi linéaire. Cet état de fait présente un intérêt notable car le courant, qui est proportionnel à la dérivée de la distribution, est alors constant et indépendant de la position. Ceci est représenté sur le schéma ci-dessous.

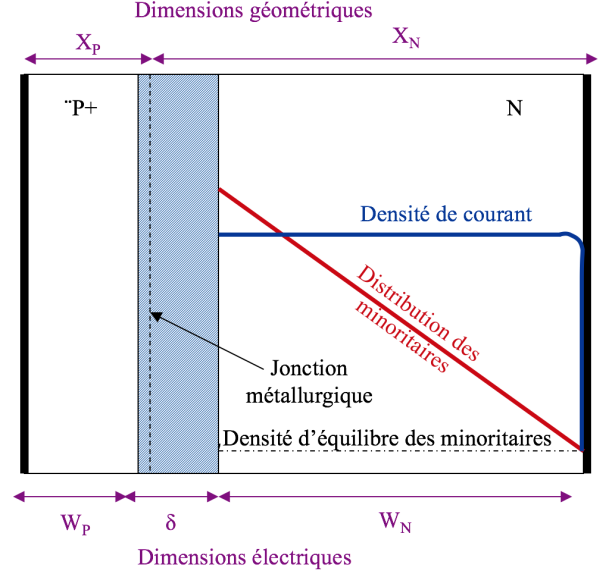
Remarque : Remarques importantes

- La charge d'espace s'étend presque exclusivement du côté le moins dopé.

- Les dimensions électriques qui interviennent dans les équations sont les dimensions effectives sur lesquelles diffusent les porteurs. Elles se déduisent des dimensions géométriques et des extensions de la charge d'espace.

- Le courant est presque exclusivement celui des minoritaires dans la région la moins dopée.

- On peut donc conclure que tout se passe du côté le moins dopé.

Méthode :

On procède donc, selon les cas (quel composant? Quelle application?), aux simplifications suivantes :

Jonction dissymétrique longue (N+ P) : $I = q A_{J} n_{i}^{2} [\frac{D_{n}}{N_{A} L_{n} th (\frac{W_{P}}{L_{n}})}] [\exp (\frac{V}{U_{T}}) - 1]$
Jonction symétrique courte : $I = q A_{J} n_{i}^{2} [\frac{D_{n}}{N_{A} W_{P}} + \frac{D_{p}}{N_{D} W_{N}}] [\exp (\frac{V}{U_{T}}) - 1]$
Jonction dissymétrique courte (N⁺ P) : $I = q A_{J} n_{i}^{2} [\frac{D_{n}}{N_{A} W_{P}}] [\exp (\frac{V}{U_{T}}) - 1]$
Jonction dissymétrique courte (P⁺N) : $I = q A_{J} n_{i}^{2} [\frac{D_{p}}{N_{D} W_{N}}] [\exp (\frac{V}{U_{T}}) - 1]$

Fondamental :

La caractéristique correspondante, pour une diode idéale est représentée sur le graphique ci-dessous.

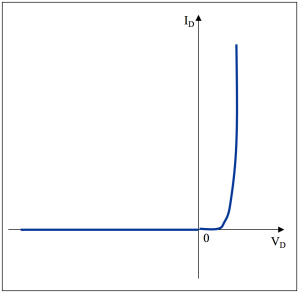
Remarque :

On peut remarquer que cet élément présente une caractéristique non linéaire:

- en direct, elle se comporte comme un interrupteur fermé,

- en inverse, comme un interrupteur ouvert.

Ainsi, les diodes ont été utilisées en logique pour réaliser des fonctions élémentaires avant l'utilisation de fonctions intégrées.