III.2 Équations caractéristiques [La jonction PN et ses applications]

III.2 Équations caractéristiques

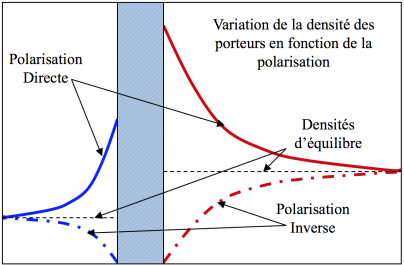
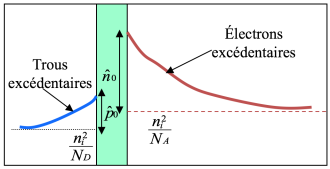
La figure ci-dessous montre la répartition des porteurs dans une jonction à l'équilibre thermodynamique en l'absence de polarisation extérieure appliquée. Les densités sont représentées en dehors de la charge d'espace.

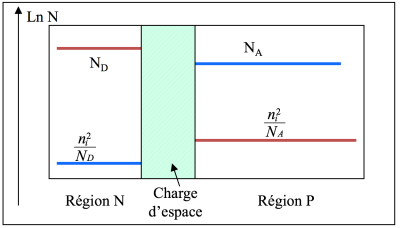
Les densités d'électrons sont reportées en rouge, celles des trous en bleu.

Si nous appliquons une tension de polarisation aux bornes de cette diode, celle ci va se superposer à la barrière de potentiel afin soit de l'augmenter soit de la diminuer.

Φ_{NP} = U_{T} Ln \frac{N_{A} N_{D}}{n_{i}^{2}} \Rightarrow \frac{N_{A} N_{D}}{n_{i}^{2}} = \exp (\frac{Φ_{NP}}{U_{T}})

$\Rightarrow \frac{n_{i}^{2}}{N_{A}} = N_{D} \exp (- \frac{Φ_{NP}}{U_{T}}) = \bar{n}$ dans la région P = minoritaires
$\Rightarrow \frac{n_{i}^{2}}{N_{D}} = N_{A} \exp (- \frac{Φ_{NP}}{U_{T}}) = \bar{p}$ dans la région N = minoritaires

Lorsque l'on polarise, la tension se retrouve en 1ère approximation aux bornes de la zce^[1] qui est un isolant. Il y a donc modification des densités de porteurs à ses limites. En effet, les densités de porteurs évoluent en exponentielle de la tension appliquée.

Les densités de porteurs minoritaires aux limites de la charge d'espace sont fonction de l'énergie qui elle même dépend du potentiel appliqué. Par exemple pour les électrons dans la région P à la limite de la zce^[1], leur densité s'écrit : $n_{0} = N_{D} \exp (- \frac{Φ_{NP} - V}{U_{T}})$ .

L'excès de densité à la limite de la zce^[1] côté P est donc :

\begin{matrix} {\hat{n}}_{0} & = & n_{0} - \bar{n} = N_{D} \exp (- \frac{Φ_{NP} - V}{U_{T}}) - \frac{n_{i}^{2}}{N_{A}} \\ = & N_{D} [\exp (- \frac{Φ_{NP} - V}{U_{T}}) - \exp (- \frac{Φ_{NP}}{U_{T}})] \\ = & N_{D} \exp (- \frac{Φ_{NP}}{U_{T}}) [\exp (\frac{V}{U_{T}}) - 1] & = \bar{n} [\exp (\frac{V}{U_{T}}) - 1] \end{matrix}

Remarque :

Il en est de même pour les trous dans la région N à la limite de la zce^[1] : $\hat{p_{0}} = \bar{p} [\exp (\frac{V}{U_{T}}) - 1]$ .

Ce qui donne finalement:

Ainsi:

Attention : Pour une polarisation en direct

La hauteur de la barrière de potentiel diminue. Par conséquent, sa largeur aussi. Les densités de porteurs aux limites de la charge d'espace vont donc augmenter :

il existe un gradient de concentration de minoritaires positifs dans la zone neutre:

on parle de porteurs en excès (injection de porteurs).

Attention : Pour une polarisation en inverse

La hauteur de la barrière de potentiel augmente. Par conséquent, sa largeur aussi. Les densités de porteurs aux limites de la charge d'espace vont donc diminuer :

il existe un gradient de concentration de minoritaires négatif dans la zone neutres:

on parle d'appauvrissement en porteurs (phénomène d'extraction).

Remarque :

En inverse, si la valeur absolue de $V$ est supérieure à quelques $U_{T}$ , $\hat{n_{0}} \approx - \bar{n} \Rightarrow n_{0} \to 0$ .

Remarque :

On obtient une équation identique pour les trous en changeant simplement n en p. Cette relation est valable quelle que soit la polarisation (directe ou inverse).

On peut remarquer en effet que:

- si $V$ est positif et grand devant $U_{T}$ , l'unité est négligeable devant l'exponentielle,

- si $V$ est négatif, c'est l'exponentielle qui est négligeable et la variation de densité est alors négative.

Ceci est illustré sur le schéma ci-dessus et explique le fait que le courant change de sens avec la polarisation (inversion du gradient de concentration) d'une part, et d'autre part que le courant inverse théorique est une constante car sa valeur dépend de l'excès de densité qui est égale, au maximum à la densité d'équilibre.