III.4 Détermination de la loi de variation de la densité des porteurs en fonction de la température
L'ionisation des impuretés va donc permettre de créer soit des électrons soit des trous dans le matériau semi-conducteur. Les densités de porteurs dans les bandes permises seront donc directement fonction de la densité des atomes d'impuretés et de leur niveau d'ionisation. Il est donc nécessaire de pouvoir définir ce degré d'ionisation en fonction de la température afin de connaître les densités de porteurs libres existant dans le matériau.
La cinétique d'ionisation des impuretés en fonction de la température, dans un semi-conducteur, est régie par la statistique de Fermi-Dirac. Par exemple, considérons du silicium dans lequel on a introduit des atomes de phosphore. Cette impureté est caractérisée par l'énergie du niveau qu'il génère (ED), et par la densité correspondante (ND en cm-3).
L'état d'ionisation des impuretés va évoluer en fonction de la température. On peut définir trois zones :
Pour T voisin du zéro absolu, le matériau est inerte et tous les porteurs sont figés sur leurs niveaux. La bande de conduction est vide et la bande de valence et le niveau donneur sont pleins.
Dès que l'on apporte de l'énergie, vu le très faible écart entre EC et ED, les impuretés vont s'ioniser faisant apparaître des électrons dans la bande de conduction. C'est la zone d'ionisation des donneurs :
Zone d'ionisation des donneurs : T ~ 0 K
L'ionisation des donneurs suit la statistique de Fermi-Dirac. On a donc :
La densité des électrons étant égale à celle des donneurs ionisés, on a donc :
La variation asymptotique est donc une droite.
La densité des donneurs étant très faible, ce niveau sera vite complètement ionisé (EC-ED = 0,04 eV).
Zone d'épuisement des donneurs
Lorsque tous les donneurs sont ionisés, la densité des porteurs reste constante tant que l'énergie n'est pas suffisante pour faire sauter des électrons de la bande de valence (EG >>EC-ED).
La densité des porteurs vaut alors: Ln (n) = Ln (ND).
Zone Intrinsèque
Lorsque la température devient suffisamment élevée, il est possible de faire passer des porteurs de la bande de valence à la bande de conduction. On génère alors des paires électron-trou. La bande de valence permettant de créer un nombre très important de porteurs , ceux issus du niveau donneur sont rapidement en quantité négligeable et le matériau se comporte alors comme un matériau intrinsèque.
Représentation graphique
Les 3 zones sont donc ainsi représentées :
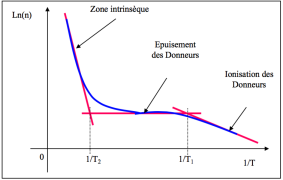
On peut déterminer les équations des asymptotes à la courbe Ln(n)= f(1/T).
L'intersection des asymptotes permet de déterminer les températures T1 et T2 qui limitent les différentes zones.
Il faut donc calculer les valeurs correspondantes afin de positionner la température ambiante.
Le calcul mené pour le silicium montre qu'elle se situe sur le plateau, dans la zone d'épuisement.
On obtient (voir calcul) T1 = 50 K T2 = 800K
Fondamental :
On peut remarquer que la température ambiante est bien au milieu du plateau. Le matériau est donc stable en température et on peut affirmer que, à température ambiante, toutes les impuretés sont ionisées.
