Dans la zone d'ionisation, la densité des atomes d'impuretés ionisées s'écrit :

$\overline{n}=N_D^{+}=N_D\mathrm{.}\frac{1}{1+\exp (\frac{E_D-E_F}{\mathit{kT}})}\approx N_D\mathrm{.}\exp \frac{-E_D-E_F}{\mathit{kT}}$

Cette expression fait apparaître le niveau de Fermi dont on ne connaît pas la position.

Il faut donc disposer d'une deuxième équation faisant intervenir celui-ci.

C'est l'équation de définition de la densité des porteurs que nous avons établi au début de ce cours :$\overline{n}=N_C\mathrm{.}\exp -(\frac{E_C-E_F}{\mathit{kT}})$

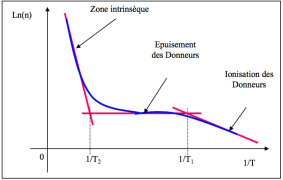
Cette 2^ème expression permet de calculer E_F. Cette expression de E_F peut alors être injectée dans la 1^ère équation donnant $\bar{n}$.

On obtient alors la loi de variation $\overline{n}=f(T)$dans cette première zone :

$\ln (\overline{n})=\frac{1}{2}\ln (N\mathrm{.}{N}_D)-\frac{E_C-E_D}{2\mathit{kT}}$

On a donc une droite de pente $\frac{E_C-E_D}{2\mathit{kT}}$ et d'ordonnée à l'origine $\frac{1}{2}\ln (N\mathrm{.}{N}_D)$

La zone d'épuisement des donneurs permet d'écrire : $\ln (\overline{n})=\ln (N_D)$

Pour la zone intrinsèque, le niveau de Fermi se situe au milieu de la bande interdite donc, E_F = (E_C+E_V)/2.

En reportant dans l'équation qui donne n, on obtient :

$\ln (\overline{n})=\ln (N)-\frac{E_C-E_D}{2\mathit{kT}}$ et d'ordonnée à l'origine ln(N).