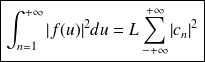Développement d'une fonction périodique en série de Fourier
Soit
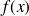une fonction périodique de période fondamentale L, on peut alors développer, sous certaines conditions (cf. théorème de Dirichlet), cette fonction en série d'exponentielles imaginaires ou de fonctions trigonométriques.
Fondamental : Série d'exponentielles imaginaires
avec
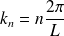et les coefficients
de la série de Fourier sont données par l'expression :
où
est un réel quelconque.
Si
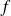est une fonction à valeur réelle, les coefficients
et
sont alors conjugués et on aura
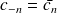
Fondamental : Série de fonctions trigonométriques
Si dans la série définie ci-dessus on regroupe les termes correspondants à des valeurs opposées de n, on obtient :
Si on pose:
pour
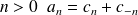
pour
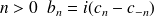
On a alors :
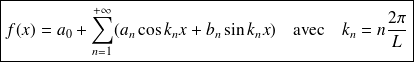
Les formules donnant les coefficients
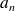et
s'en déduisent :
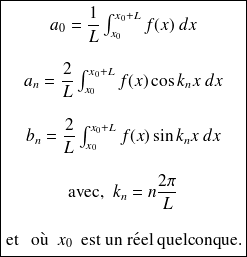
Si
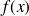est paire, les
sont nuls, si
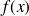est impaire
et les
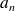sont nuls.
Si
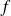est une fonction à valeurs réelles, alors on aura
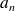et
réels.
Fondamental : Théorème de Dirichlet
Soit
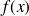une fonction périodique,
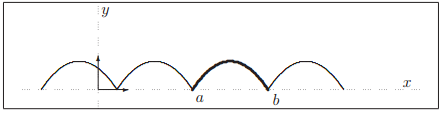
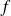vérifie les conditions de Dirichlet si elle est continue par morceaux et admet un dérivée continue par morceaux telle que en tout point la dérivée admette une limite à gauche et à droite. Alors la série de Fourier converge et l'on a :
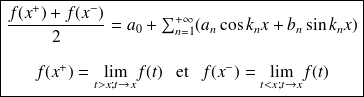
Si
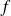est continue en
on aura donc :
Fondamental : Egalité de Bessel Parseval
Soit
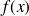une fonction périodique de période fondamentale L. Alors on démontre que :
