Fonctions périodiques
Définition :
Une fonction
de variable réelle est dite périodique s'il existe un réel
non nul tel que :
est appelé période de la fonction
. La période fondamentale est la plus petite valeur positive
de L possible. Si L une période, alors
est aussi une période de
. On utilise toujours
le terme de période en physique et en chimie pour désigner la période fondamentale.
Exemple :
Exemples :
la fonction
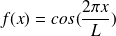est périodique de période L.
Le fonction
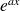est périodique de période L si :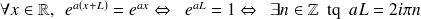
A partir d'une fonction
définie seulement sur un intervalle
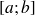de l'axe réel, on peut construire la fonction
périodique égale à f sur cet intervalle, définie sur
, et de période
.
