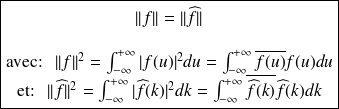Transformée de Fourier
Définition :
La transformée de Fourier
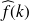d'une fonction
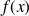est définie par :
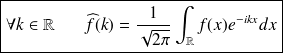
Propriétés
Rappel : Parité
Si f est paire,
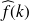est paireSi f est impaire,
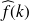est impaireSi f est réelle paire,
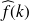est réelle paireSi f est réelle impaire,
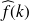est imaginaire pure et impaire
Rappel : Conjugaison
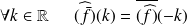
Donc si
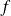est à valeurs réelles :
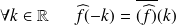
Définition : Transformée de Fourier inverse
Comme on a défini la transformée de Fourier directe, on peut définir la transformée de Fourier inverse par :
Et l'on a, pour les points
où
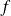est 'assez' régulière :
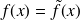
Fondamental : Formule de Parseval-Plancherel
Sans rentrer ici dans les espaces de fonctions, les normes et notions de convergence, il vous
faut retenir que la transformation de Fourier conserve la norme, c'est-à-dire que l'on a :
