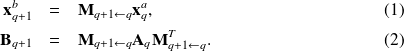Kalman's Filter: I equations
What is this cycle for Gaussian statistics and linear dynamics?
We have to model error. This is done as follow
The prior distribution
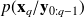takes the form
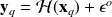where
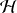, the observational operator, mapps the model space
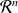into the observational space
,
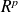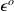is the observational error and we assume it is a Gaussian random variable, centered, and of covariance matrix
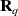, hence, its distribution is no more than
So what is the plan?
First, we have to detail the analysis step.
then the forecast step
Let start with the analysis step!
analysis step
We apply the Baye's rule within the analysis step, and obtain that
Where
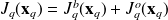
is the likelihood
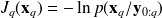with
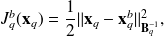
the background term and the observational term
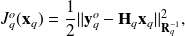
where
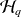is assumed to be linear, and denoted by
.
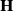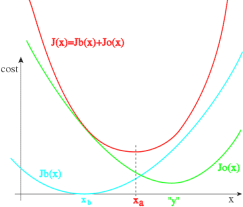
In the 1D framework, this corresponds to the scheme
The analysis
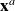is not too far from the background
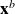and not too far from the observations
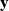
Since
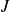is quadratic, then it must exists
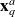and
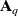such that
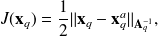
within a constant (not important due to the normalization).
We have to fi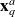nd
and
:
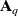Due to the quadraticity of cost function
,
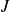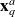is the unique miminum of
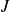, that is the point that nullify the gradient of
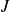.Again, the quadraticity leads that the Hessian of
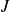(that is the second order derivative of
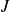along
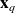) is the inverse of the matrix
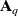
We find these quantities as follow...
It is easy to find
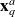thanks to the change of variable
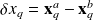leading to the incremental formulation
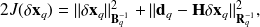
where
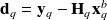is the innovation.
Then, the gradient of
,
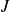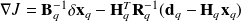is null in
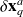means that
and the computation of the Hessian
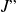, then its inverse, leads to
Analysis step
We have obtained that in the Gaussian case, the analysis step provides that
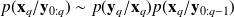leads to
with
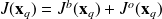is a quadratic cost function of unique minimum
where
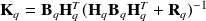and analysis covariance matrix
forecast step
Now we are interested by the forecast step.
By definition,
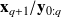is deduced from the time evolution where the linear dynamics implies
Since the linear transform of a Gaussian is also Gaussian, we obtain that the distribution
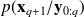is the Gaussian
Where
and
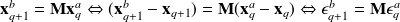
leads to
Forecast step
Under linear dynamics and Gaussian distribution, the forecast step provides that
with
and
Hence, for Gaussian distribution and linear dynamics,
Fundamental : Kalman's filter equations
Analysis step:
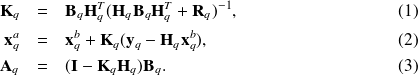
Forecast step:
