Etude des séries à terme positifs
Dans toute la suite 
désignera une série où la suite 
est à termes réels positifs (sauf, peut-être les 
premiers termes, étant un entier naturel fixé, car la nature d'une série - convergente ou divergente - n'est pas modifiée si l'on supprime les premiers termes).
Séries de référence
Définition : (Séries de Riemann)
Toute série de la forme 
est appelée série de Riemann.
Fondamental : Propriété
converge si et seulement si 
Définition : (Séries géométriques à termes positifs)
On appelle série géométrique à termes positifs toute série de la forme 
où 
est un réel positif.
Fondamental : Propriété
Soit une série géométrique à termes positifs. converge si et seulement si 
. Auquel cas :
Critères de comparaison des séries à termes positifs
Fondamental : Théorème
converge si et seulement si la suite des sommes partielles 
est majorée.
En effet, la suite des sommes partielles est croissante. Si cette suite est majorée, alors elle converge.
Fondamental : Théorème (critère de majoration ou minoration)
Soient et 
deux séries à termes positifs.
On suppose que : à partir d'un certain rang 
. Alors :
Si la série
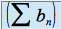converge alors la série 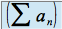converge.Si la série
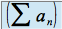diverge alors la série 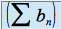diverge.
Fondamental : Théorème (critère d'équivalence)
Soient deux séries à termes positifs. Si 
est équivalent à au voisinage de 
alors et sont de même nature.
Règle de Riemann
Comment procéder de manière pratique pour comparer une série à termes positifs avec une série de Riemann ?
Soit une série à termes positifs.
On commence par chercher un équivalent de 
au voisinage de le plus simple possible, qu'on appelle 
. Deux cas sont possibles :
Premier cas : Si
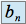est de la forme 
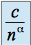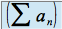alors et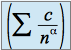 
sont de même nature.Deuxième cas :
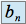n'est pas de la forme 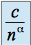, on utilise alors la règle suivante.
Fondamental : Propriété (règle de Riemann)
On calcule 
.
si
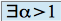tel que 
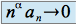quand 
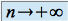(où 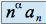est majorée) alors 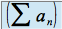converge.si
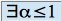tel que 
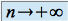quand (où 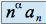est minorée par un réel strictement positif) alors 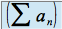diverge.
Remarque : Cette règle ne permet pas de conclure dans toutes les situations.
Règle de d'Alembert
Fondamental : Propriété
Soit une série à valeurs positives.
On suppose que 
.
On suppose de plus que 
converge vers une limite 
finie ou non.
Si
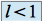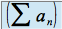alors convergeSi
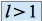alors 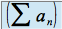divergeSi
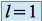alors on ne peut pas conclure. Ce cas est appelé cas douteux de la règle de d'Alembert.
