Définitions et généralités
Soient 
une suite à valeurs dans 
. A on peut associer une suite
Définition :
On appelle série de terme général 
, que l'on note 
, la suite 
de nombres réels définie par :
est appelé terme général de la série
est appelée somme partielle des 
premiers ou nième somme partielle de la série
est appelée suite des sommes partielles de la série
Définition :
Soit une série à termes réels. On dit que la série
converge lorsque la suite des sommes partielles de la série converge.
En cas de convergence, 
est notée 
et est appelée somme de la série.
Un série qui ne converge pas est dite divergente.
Définition :
Si une série converge vers , on appelle suite des restes la suite 
définie pour tout entier naturel par 
On a donc :
Exemple
Exemple :
Soit la série de terme général 
, 
On a :
et
donc la série de terme général converge et :
Exemple
Exemple :
Soit la série de terme général 
La suite définie par 
est une suite géométrique de premier terme 
et de raison 
.
On a :
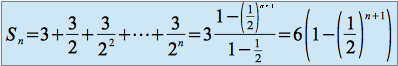
et
donc la série de terme général converge et :
Note : on dit que la série 
est une série géométrique.
