Croissance comparée de e^x, x^α et ln x
Fondamental : Théorème
![]() est un réel strictement positif, les fonctions
est un réel strictement positif, les fonctions ![]() ,
, ![]() et
et ![]() ont pour limite
ont pour limite ![]() en
en ![]() , et on a :
, et on a :
De plus
On dit, par abus, que, lorsque ![]() tend vers
tend vers ![]() , les puissances positives d'un réel positif "l'emportent" sur la fonction ln, et que la fonction exponentielle "l'emporte" sur toute puissance positive d'un réel positif.
, les puissances positives d'un réel positif "l'emportent" sur la fonction ln, et que la fonction exponentielle "l'emporte" sur toute puissance positive d'un réel positif.
Exemple :
Calculer : 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]()
On écrit :
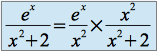
Or
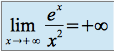 et
et 
donc
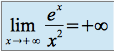
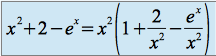
on a :
 et
et 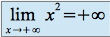
donc
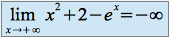
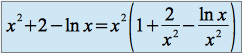
on a :
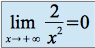 et
et 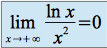
donc

enfin






