Fonctions puissances
Définitions et propriétés
Définition :
Pour tout 
réel strictement positif, et tout réel 
on pose :
Remarque :
Cette définition est cohérente avec la définition usuelle des puissances entières. En effet, étant un réel strictement positif, on peut écrire, par exemple :
Elle donne un sens à des écritures telles que 
ou encore 
.
Attention, cependant, lorsque est réel, l'écriture 
n'est possible que si 
Les propriétés de la fonction exponentielle permettent d'écrire :
Fondamental : Propriété
Pour tous réels et 
strictement positifs, et pour tous réels 
et 
:
Exemple :
Résoudre dans 
: 
Pour tout réel, on a : 
Soit 
, ce que l'on peut écrire : 
On obtient : 
, finalement :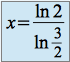 
Cas particulier des racines n-ièmes
Soit un réel strictement positif et 
un entier naturel non nul, on a :
En effet, on a : 
, donc 
Or 
, donc :
Enfin, 
, ce qui s'écrit :
Exemple :
Calculer 
