Définition
Définition :
Il existe une unique fonction
dérivable sur 
telle que :
On la nomme fonction exponentielle, on note, pour tout 
réel :
Remarque :
Par définition, 
Ce nombre 
est un nombre réel, irrationnel, 
Fondamental : Propriété
Quel que soit
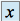réel, 
et 
La fonction
est dérivable et donc continue sur et 
Pour tous réels
et 
et pour tout entier relatif 
:
Exemple :
Simplifier 
; 
; 
;
Finalement
