Suites et séries
Suites et séries
Question
Etudier dans chaque cas la convergence des suites
et des séries suivantes définies par leur terme général :
En multipliant par l'expression conjuguée au numérateur et au dénominateur, on obtient :
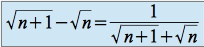
donc la suite converge vers
. Mais si nous calculons les sommes partielles, par télescopage (les termes s'éliminent deux à deux, il ne reste que le premier et le dernier) on obtient :
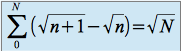
ce qui implique la divergence de la série.
Si
est pair,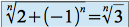 
et si est impair :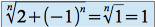 
Les suites extraites respectivement d'indices pair et impair, convergent vers la même limite :
qui n'est pas nulle. On déduit donc que la suite converge vers et la série diverge.Il est utile de connaître
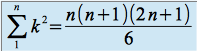, le terme général de la suite s'écrit donc :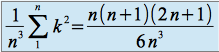
et converge vers
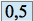. La série ne peut donc converger.
