Suite réelle
Suite réelle
Soit :
Question
Pour tout entier naturel
, justifiez l'existence de 
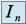.Etudier la monotonie de la suite de terme général
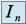.Montrer que pour tout entier naturel non nul :
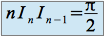.Montrer que la suite
converge, en déduire sa limite.
Pour tout
de l'intervalle d'intégration :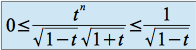 
Or
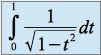converge donc par majoration, l'intégrale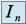converge.La suite de terme général
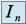est décroissante en effet :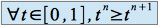 
donc
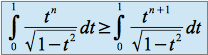
Il suffit de démontrer la relation
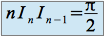par récurrence.Pour
, on a :
et
Ainsi :
Supposons la relation vraie au rang
, soit :
Effectuons une intégration par parties sur
:
D'où, en séparant cette intégrale en deux parties :
soit
en multipliant par
, on obtient : 
La suite
est décroissante, minorée par 
donc convergente.En passant à la limite dans l'expression :
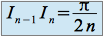, on déduit que la limite est .
