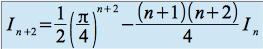Suite réelle
Suite réelle
Pour tout entier naturel 
, on pose :
Question
Sans calculer
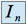montrer que la suite 
est monotone et comparer 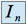et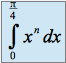 
.Calculer la limite de la suite
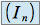.Calculer
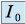et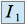 
. Exprimer 
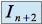en fonction 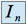de et de .
On a :
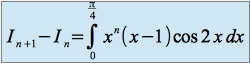.on sait que
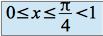, et donc 
, 
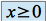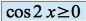et 
.Par conséquent :
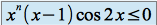, et donc 
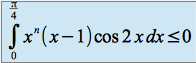.On en déduit que
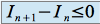, la suite 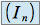est donc décroissante.
, 
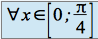d'où :
On en déduit
et donc
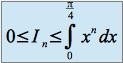
A partir du résultat précédent, on peut écrire :
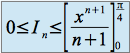
et donc :
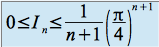
On a donc
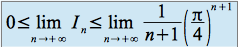d'où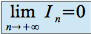 
Calcul de
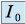et de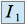
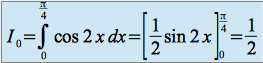
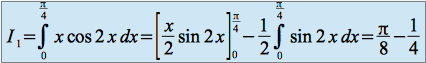
Pour obtenir
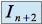en fonction de 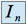il faut effectuer deux intégrations par parties successives :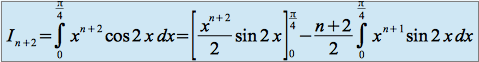
et
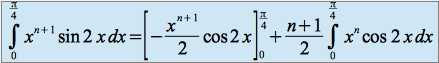
On obtient finalement :
