Séries numériques
Séries numériques
Soit 
un réel positif, considérons les séries suivantes : 
et 
Question
A quelle condition (sur
) ces séries sont-elles convergentes ? En supposant que
satisfait la condition précédente, calculer 
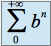et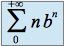 
.
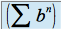- est une série géométrique qui converge si et seulement si
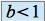(voir cours).La règle d'Alembert pour les séries numériques permet de conclure que
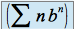converge si et seulement si 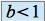. Supposons donc
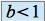
pour la première série :
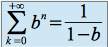
pour la deuxième série, calculons
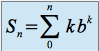sous la forme :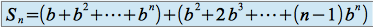 
On obtient :
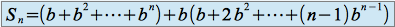
Soit :
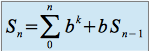
Donc :
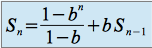
On passe alors à la limite, on obtient :
