Equation différentielle linéaire à coefficients constants
Introduction
On cherche les solutions aux équations du type :
où 
et 
sont des constantes réelles et 
Nous débuterons par l'étude des équations homogènes (i.e. avec un second membre nul). Puis en utilisant les résultats, nous verrons comment résoudre les équations avec second membre.
Equation homogène
Soit l'équation à résoudre :
où
et
sont des constantes réelles et .
Supposons que 
, 
alors, nous pouvons écrire :
Intégrons par rapport à 
. La primitive du membre de gauche est : 
, donc nous obtenons :
où 
est une constante réelle qui tient compte des constantes d'intégration des deux membres.
Prenons l'exponentielle de la relation précédente, on obtient :
Or 
, d'où :
est une constante réelle positive. Soit 
cette constante. On a alors :
L'expression 
représente une constante positive ou négative, notons 
cette constante réelle.
On a alors :
Nous obtenons donc une famille de fonctions. La constante pourra être calculée pour répondre à un cas précis à partir, par exemple, d'une condition particulière du type : 
.
Exemple
Résoudre l'équation
en prenant la condition
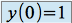
en prenant la condition
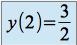
Solution
Partons de l'équation différentielle :
en supposant que , , nous pouvons diviser cette équation par 
, soit :
soit :
soit :
soit :
La constante dépend de la condition initiale :
pour
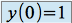, on obtient 
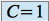, soit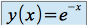 
pour
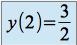, on obtient 
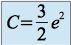, soit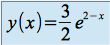 
Equation avec second membre
L'équation différentielle du premier ordre à coefficients constants avec second membre s'écrit :
où
et
sont des constantes réelles et .
Propriété
(Méthode de variation de la constante) La méthode de résolution se décompose en trois points :
on résout l'équation homogène, la solution générale est de la forme :
, , 
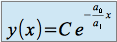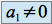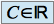
On considère que la constante
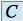dépend de 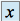(d'où le nom de la méthode : méthode de la variation de la constante), on pose :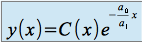
on dérive, on reporte dans l'équation avec second membre et on résout l'équation différentielle d'inconnue
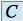.la solution générale de l'équation complète est obtenue en remplaçant
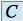par la famille de primitives trouvée au point précédent.
Application
Appliquons cette méthode sur le cas général. Calculons la dérivée de : .
On obtient :
En injectant cette expression dans l'équation différentielle à résoudre, nous obtenons :
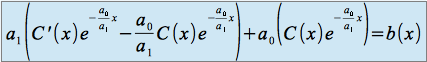
soit :
soit :
En intégrant, on obtient :
Si on peut calculer explicitement cette intégrale, on en déduit la forme générale de la solution :
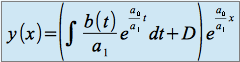
La valeur de 
est obtenue à partir d'une condition aux limites.
Exemple
Exemple :
avec la condition initiale 
L'équation homogène associée est :
Sa solution a été déterminée dans l'exercice précédent, nous avons donc :
Supposons à présent que dépend de la variable . On a alors : 
.
En injectant ces expressions dans l'équation différentielle, nous obtenons :
Soit :
Une primitive particulière de 
peut s'écrire :
d'où
L'expression générale de la solution de l'équation différentielle est donc :
La constante peut être calculée à partir de la condition initiale . On obtient alors :
d'où . La solution est donc :
