Famille libre
Définition :
On dit qu'une famille finie de vecteurs 
d'un espace vectoriel 
est libre si et seulement si aucun des vecteurs de cette famille n'est combinaison linéaire des autres. Ceci est aussi équivalent à :
.
Exemples
Exemple :
Dans 
, soient les vecteurs 
, 
et 
. La famille 
est une famille libre dans . En effet, supposons qu'il existe des réels 
tels que 
C'est dire :
On a donc
Ce qui donne immédiatement 
Exemple :
Dans , soient les vecteurs , et 
. La famille n'est pas une famille libre dans car 
. On dit que cette famille est liée.
Exemple :
Soit 
. 
est un s.e.v. de .
Soit 
, on a donc : 
, et tout élément 
s'écrit donc comme :
Ainsi, les vecteurs 
et 
forment une famille génératrice de . De plus 
s'écrit 
, ce qui revient à 
et est équivalent à 
.
La famille 
est donc une famille libre dans .
Fondamental : Propriété
Toute sous famille d'une famille libre est libre.
Toute famille contenant une famille liée est liée.
Toute famille
dont l'un des vecteurs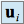 
est nul est liée.
