Base d'un espace vectoriel
Base d'un espace vectoriel
Dans l'ensemble 
des polynômes à une indéterminée, à coefficients réels, et de degré inférieur ou égal à 2, on définit une loi de composition interne, notée 
, et une loi de composition externe notée 
, telles que :
.
Question
Montrer que l'ensemble , muni de ces deux lois, est un espace vectoriel sur 
.
Les propriétés de l’addition des réels nous permettent d'écrire :
et
.
Le polynôme nul 
est l'élément neutre.
Le polynôme, noté 
, de coefficients 
est l'élément symétrique du polynôme 
de coefficients 
.
est donc un groupe commutatif.
Soient et 
éléments de , 
, on vérifie les quatre propriétés suivantes :
.
.
.
.
L'ensemble , muni de ces deux lois, est donc un espace vectoriel sur .
Question
Soient 
les polynômes de définis par :
.
Montrer que 
est une base de (qui est d'ailleurs appelée base canonique de ).
étant un polynôme de , il existe trois réels tels que, pour 
, on puisse écrire :
soit 
.
La famille est donc une famille génératrice de .
De plus, cette famille est libre. En effet, 
si et seulement si :
,
c'est à dire :
.
est donc une base de .
Question
Soient 
les polynômes de définis par :
.
Montrer que
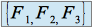est une base de 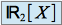.Déterminer dans cette base les coordonnées des polynômes
et 
définis par :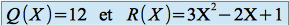
L'espace vectoriel
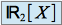étant de de dimension 3, il suffit alors de montrer que 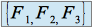est une famille libre pour pouvoir affirmer que c'est bien une base.Soient trois réels
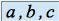, tels que :
.
On a donc :
,
ou encore :
.
On en déduit donc que :
,
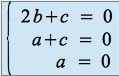qui équivaut à : .
Ainsi est une famille libre, et c'est bien une base de .
Soient
les coordonnées de dans la base 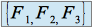.On peut donc écrire :
.
Or les coordonnées de dans la base canonique sont 
. On en déduit :
,
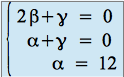ce qui équivaut à :
.
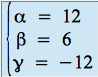Les coordonnées de dans la base sont donc : 
.
De même pour , on obtient :
,
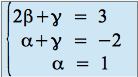qui équivaut à :
.
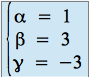Les coordonnées de dans la base sont donc : 
.
