Structure d'espace vectoriel
Structure d'espace vectoriel
Un espace vectoriel original.
Question
Prouver que 
est un groupe abélien (“·” est la multiplication habituelle, il faut vérifier que “·” est interne et vérifie les propriétés 
).
Soient 
et 
. On a : 
, et la loi “·” est donc interne.
La loi “·” est (de manière évidente) commutative et associative dans 
.
Il est clair que 
est élément neutre, car en effet : 
.
On a aussi, 
, et 
est l'élément symétrique de 
, puisque
.
En conclusion, est un groupe abélien.
Question
On définit dans une loi externe, notée 
, de la façon suivante :
Montrer que 
est un espace vectoriel sur 
.
Soient 
et 
. On vérifie aisément les quatre propriétés suivantes :
.
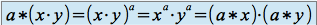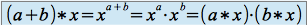(attention, la loi interne du groupe n'est pas la même que la première loi du corps de référence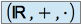 
).
.
.
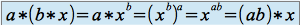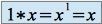Ainsi, est bien un espace vectoriel sur .
Question
Montrer que tout élément 
engendre .
Pour prouver que tout élément engendre , il faut montrer que tout élément de s'exprime linéairement en fonction de 
, c'est à dire :
Or
Donc pour , on peut écrire
,
d'où on peut conclure que tout élément engendre .
