Matrices - déterminants
Matrices - déterminants
Utilisation du déterminant pour calculer le rang d'un système de vecteurs.
Question
Soit la matrice à coefficients réels 
Expliquez sans calculs pourquoi le rang de 
est supérieur ou égal à 2 et inférieur ou égal à 3.
Comment choisir 
, 
et 
pour que le rang soit 2 ?
On sait que et 
ont le même rang.
ayant 4 colonnes, 
;
ayant 3 colonnes, 
De plus les deux vecteurs colonnes du milieu 
ne sont pas colinéaires donc 
.
Il faut choisir 
pour que le rang soit égal à 2 donc que les vecteurs colonnes 1 et 4 soient combinaisons linéaires des vecteurs colonnes 2 et 3.
Ce qui revient à dire que les déterminants 
et 
sont nuls.
Ce qui s'écrit 
On vérifie que ces conditions nécessaires sont suffisantes.
Question
Trouver une base de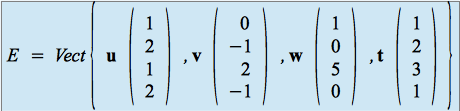 
Les deux premiers vecteurs ne sont pas colinéaires car leurs coordonnées ne sont pas proportionnelles. On peut le voir en remarquant que le déterminant extrait de leurs coordonnées est non nul. 
Pour savoir si le troisième vecteur 
est combinaison linéaire des deux premiers, on peut chercher s'il existe deux réels et tels que : 
. On peut aussi voir si la famille 
est liée, s'il en est ainsi tous les déterminants de format 
extraits de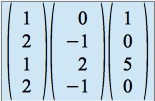 
sont nuls.
Or :
La famille est donc liée. Le 3ème vecteur est combinaison linéaire des deux premiers
Appliquons la même méthode pour savoir si 
appartient à 
Si la famille 
était liée, tous les déterminants de format extraits de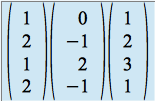
seraient nuls.
Or, 
Donc cette famille est libre et est une base de de l'espace vectoriel 
qui est donc de dimension 3.
