Applications 5
Exercice 1
Enoncé
Un tube d'acier de 10 cm de diamètre extérieur est parcouru par de la vapeur d'eau saturée à 160 °C. Ce tube est calorifugé par de la terre infusoire dont la conductivité thermique varie en fonction de la température suivant l'expression : λ (kcal.h-1.m-1.°C-1) = 0,82 + 0,0008 θ (°C) L'épaisseur du revêtement est de 5 cm. On demande de calculer la quantité de vapeur d'eau condensée par heure et par mètre de longueur de tube si le milieu extérieur est à 10 °C. On donne : -coefficient superficiel d'échange entre la surface du calorifuge et le milieu extérieur : h = 10 kcal.h-1.m-2.°C-1. -chaleur latente de condensation de la vapeur d'eau à 160 °C : ΔHcond = 500 kcal.kg-1. On supposera que le condensat n'est pas sous refroidi et que la surface extérieure du tube d'acier se trouve à 160 °C. |
|---|
Solution
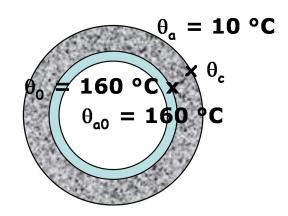
Flux de chaleur échangé :
avec θm = 0,82 + 0,0008 (θ0 + θc)/2 = 0,884 + 0,0004 θc Soit θc = 95,6 °C D'où Q/L = h . 2π . (R + e) . (θc – θa) = 10 . 2π . 0,1 . (95,6 – 10) = 537,84 kcal.h-1.m-1 Quantité d'eau condensée : M = Q / ΔHcond = 537,84 / 500 = 1,08 kg.h-1.m-1 . Remarque : Si le tube n'était pas calorifugé, le flux de chaleur serait : Q/L = h . 2π . R . (θ0 – θa) = 471,24 kcal.h-1.m-1 et la quantité d'eau condensée serait égale à 0,942 kg.h-1.m-1 c'est-à-dire moins qu'avec le tube calorifugé. Cela est dû au fait que le calorifuge ne convient pas (mauvaise conductivité thermique ; problème de rayon critique). |
.
Exercice 2
Enoncé
La voûte d'un four, de forme semi cylindrique doit être composée de deux couches de briques : l'une de briques réfractaires de conductivité thermique λ1 = 0,9 + 0,0002 θ (λ en W.m-1.°C-1 et θ en °C) l'autre de briques isolantes de conductivité thermique λ2 = 0,5 + 0,0003 θ (λ en W.m-1.°C-1 et θ en °C) La surface interne de la voûte, dont le rayon est de 3 m, se trouve à 1400 °C et la face externe est en contact avec de l'air dont la température sera prise égale à 10 °C. Le coefficient superficiel d'échange entre la face externe de la voûte et le milieu ambiant est h = 18 W.m-2.°C-1. Sachant que l'on veut limiter les pertes thermiques vers le milieu ambiant à 1260 W par m2 de surface extérieure de voûte, on demande de déterminer l'épaisseur de chaque couche de brique pour que l'épaisseur totale de la paroi soit minimale et que la température des briques isolantes n'excède pas 1000 °C. |
|---|
Solution

Données : Q/Aextérieure = q = 1260 W/m2 θ briques isolantes < 1000 °C Attention : aire d'échange = demi cylindre . Expressions des flux de chaleur :
. A partir de l'équation (3), on peut écrire : θ2 = θa + q/h Soit : θ2 = 10 + 1260 / 18 = 80 °C . Il faut que l'épaisseur totale soit minimale, c'est-à-dire que r2 soit minimum, tout en limitant les pertes thermiques et θ1 < 1000 °C. (1) => (2) => (4) + (5) => . Pour satisfaire aux contraintes fixées ci-dessus, il faut que q . r2 . Ln(r2/r0) soit minimal, soit :
-0,9 + 0,0001 (θ0 –θ1) – 0,0001 (θ0 + θ1) + 0,5 + 0,00015 (θ1 – θ2) + 0,00015 (θ2 + θ1) = 0 -0,4 + 0,0001 θ1 = 0, soit θ1 = 4000 °C Si θ1 < 4000°C, r2.ln(r2/r0) est décroissant Si θ1 > 4000°C, r2.ln(r2/r0) est croissant Comme θ1 ne doit pas être supérieur à 1000 °C et que r2.ln(r2/r0) doit être le plus faible possible, la limite est donc 1000 °C. On calcule alors e1 et e2. (6) => ln(r2/r0) = [(0,9 + 0,0001 . 2400) . 400 + (0,5 + 0,00015 . 1080) . 920] / (1260.r2) soit r2 = 3,757 m (4) => ln( r1/r0) = [(0,9 + 0,0001 . 2400) . 400] / (1260.r2) soit r1 = 3,303 m . Comme r0 = 3 m, e1 = 0,303 m et e2 = 0,454 m |
.





