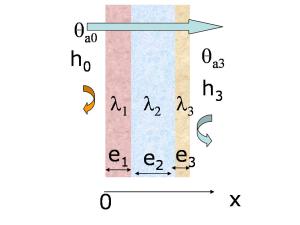
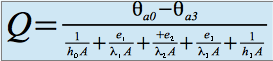Cas du mur composite
On appelle mur composite la juxtaposition de plusieurs murs simples constitués de matériaux différents, limités par des plans parallèles et en contact parfait les uns avec les autres. Considérons par exemple un mur composite formé par la juxtaposition de trois murs simples dont les épaisseurs et les conductivités thermiques, indépendantes de la température, sont définies sur le schéma ci-contre. Les parois extrêmes échangent par convection avec des milieux fluides (h coefficient de convection, θa températures des fluides, A surface des parois). Il est facile de généraliser les résultats précédents. Le flux à travers la surface A est donné par :
|  . |
Remarque :
Chaque terme exprimé au dénominateur dans l'équation ci-dessus est appelé résistance thermique.
Cas où la conductivité thermique dépend de la température
La conductivité thermique du matériau peut varier avec la température. D'une manière générale, cette variation est linéaire :
λ = λ0 (1 + aθ) .......................................................................(équation 40) |
En reprenant la démonstration établie pour le mur simple et en intégrant la variation de la conductivité thermique, on obtient :
|
n'est autre que la conductivité thermique λm du matériau prise à la température moyenne (θ0 + θ1)/2.
On peut ainsi écrire :
|
Quant au profil de température, il peut être déterminé à partir de l'équation :
|
Application 2
Exercice 1
Enoncé
La paroi d'un mur est à 200 °C. Elle est calorifugée par 10 cm de laine de verre de conductivité thermique λ (W.m-1.K-1) = 0,025 + 5.10-5 θ (°C) La face externe du calorifuge est à 26 °C. Calculer le flux de chaleur par unité de surface. |
|---|
Solution
Q = {0,025 + [5.10-5. (200 + 26) / 2]} . (1 / 0,1) . (200 – 26) = 53,3 W.m-2 |
.
Exercice 2
Enoncé
La paroi d'un grand four plat est composée de trois couches : - 10,0 cm de briques réfractaires en kaolin à l'intérieur, - 12,5 cm de briques isolantes en kaolin au milieu, - 12,5 cm de briques de magnésie à l'extérieur. La surface intérieure est à 745 °C. Si l'air ambiant est à 30 °C et si l'on admet un coefficient superficiel d'échange h = 30 W.m-2.K-1 à la paroi extérieure, quelles sont les pertes thermiques et la température de la face extérieure du four ? Données : Briques réfractaires à l'intérieur : λ1 = 0,87 W.m-1.K-1 Briques isolantes au milieu : λ2 = 0,60 W.m-1.K-1 Briques de magnésie à l'extérieur : λ3 = 1 W.m-1.K-1 |
|---|
Solution
. |  . |
