Introduction to Data Assimilation for Scientists and Engineers

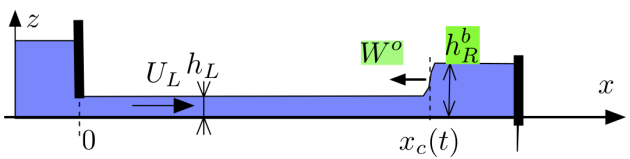
One assumes that the informations \(h_R^b\) and \(W^o\) are independant:

• Control space: \(x= h_R\)

• Background: \(x^b = h_R^b\) with root mean square error \(\sigma_b= \sigma_{h_R^b}\)

• Measurements: \(y = W^o\) with root mean square error \(\sigma_r = \sigma_{W^o}\)

• Observation operator: \(\displaystyle y = {\cal G}(x) = - {q \over x -h_L}\)

The cost function to minimize to find the analysis \(x^a = h_R^a\) is \(\displaystyle J(x) = { (x- x^b)^2 \over 2\, \sigma_b^2} + { [ y^o - {\cal G}(x)]^2 \over2 \, \sigma_r^2}\)