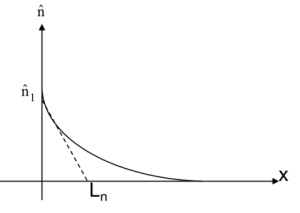
III.3 Longueur de diffusion

Considérons maintenant un semi conducteur excité de manière homogène en surface, en régime permanent.

Le rayonnement impose en surface des porteurs en excès n ^ = p ^ hat n = hat p

Les équations de continuité deviennent :

dn dt = 0 = D n d 2 n dx 2 + 0 + 0 + g − n ^ τ dn over {dt} = 0 = D_{n} {d ^{2}n} over {dx ^{2}}+0+0 +g-hat n over %tau

Si le rayonnement est peu pénétrant, gn = 0 dans le volume, donc :

D n d 2 n dx 2 = n ^ τ D_{n} {d ^{2}n} over {dx ^{2}} = hat n over %tau

Définition

Soit Ln la longueur de Diffusion des électrons : L n = D n . τ L _{n} = sqrt{{ D _{n} .%tau}}

d 2 n dx 2 = n ^ L n = d 2 n ^ dx 2 {d ^{2}n} over {dx ^{2}} = hat n over L _{n} = {d ^{2}hat n} over {dx ^{2}}

Définition

De même Lp la longueur de Diffusion des trous : L p = D p . τ L _{p} = sqrt{{ D _{p} .%tau}}

d 2 p dx 2 = p ^ L p = d 2 p ^ dx 2 {d ^{2}p} over {dx ^{2}} = hat p over L _{p} = {d ^{2}hat p} over {dx ^{2}}

En intégrant ces équations avec

n ^ = p ^ = p 1 ^ = n 1 ^ en x = 0, et n ^ = p ^ = 0 quand x → ∞ hat n = hat p = hat p _{1} = hat n _{1} en x=0, et hat n = hat p ~=0 ~quand x toward infinity

Fondamental

p ^ = p 1 ^ . exp ( − x L p ) et n ^ = n 1 ^ . exp ( − x L n ) hat p = hat p _{1}.exp ( {-x} over {L _{p}}) ~et ~ hat n = hat n _{1}.exp ( {-x} over {L _{n}})